leetcode官方题库
1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出和为目标值 target 的那两个整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案。
示例 1:输入:nums = [2,7,11,15], target = 9,输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1]。
示例 2:输入:nums = [3,2,4], target = 6,输出:[1,2]
示例 3:输入:nums = [3,3], target = 6,输出:[0,1]
解题思想1:暴力解决,两层遍历,判断两数之和是否等于target
var twoSum = function(nums, target) {
let res = []
if (nums.length === 0) {
return res
}
for (let i = 0; i < nums.length; i++) {
for (let j = i+1; j < nums.length; j++) {
if (nums[i] + nums[j] === target) {
res.push(i)
res.push(j)
return res
}
}
}
return res
};解题思想2:创建一个哈希表,对于每一个nums[i],首先查询哈希表中是否存在 target - nums[i],然后将 nums[i] 插入到哈希表中,即可保证不会让 nums[i] 和自己匹配。
var twoSum = function(nums, target) {
let res = [];
if (nums.length === 0) {
return res;
}
let map = new Map();
for (let i = 0; i < nums.length; i++) {
if (map.has(target-nums[i])) {
return [map.get(target-nums[i]), i];
}
map.set(nums[i], i);
}
return res;
}2. 两数相加
给你两个非空的链表,表示两个非负的整数。它们每位数字都是按照逆序的方式存储的,并且每个节点只能存储一位数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例1:输入:l1 = [2,4,3], l2 = [5,6,4],输出:[7,0,8]
解释:342 + 465 = 807
示例 2:输入:l1 = [0], l2 = [0],输出:[0]
示例 3:输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9],输出:[8,9,9,9,0,0,0,1]
时间复杂度 O(n) 空间复杂度O(1)
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} l1
* @param {ListNode} l2
* @return {ListNode}
*/
/**2两数相加 */
var addTwoNumbers = function(l1, l2) {
let res = new ListNode() //结果链表
let cur = res
let total = 0 //节点相加得到的和
let next1 = 0 //是否需要向下一位进1
let num1 = 0 //当前两个链表的节点值
let num2 = 0
while(l1 !== null || l2 !== null){
num1 = l1 === null ? 0 : l1.val
num2 = l2 === null ? 0 : l2.val
total = num1 + num2 + next1
cur.next = new ListNode(total % 10) //新建节点,取总和的个位数进行赋值
next1 = parseInt(total / 10) //取十位数
//遍历节点
if(l1 !== null){
l1 = l1.next
}
if(l2 !== null){
l2 = l2.next
}
cur = cur.next
}
if(next1 != 0){
//说明此时还有一个数没有加上
cur.next = new ListNode(next1)
}
return res.next
};5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:输入:s = “babad”,输出:”bab”
解释:”aba” 同样是符合题意的答案。
示例 2:输入:s = “cbbd”,输出:”bb”
示例 3:输入:s = “a”,输出:”a”
示例 4:输入:s = “ac”,输出:”a”
解题思想1:动态规划,一旦在一个回文串的两端,对称的加上相同的元素,那么新形成的字符串仍然是一个回文串。设定两个下标i,j,从左往右扫描,一旦i,j下标重合,那么i下标移动到头部,从头开始扫描,j下标向后移动元素。当i,j下标指向的元素相同的时候,判断除去这两个相同的元素剩下的字符串是不是一个回文串,如果是,那么当前最长回文串就是当前形成的串,如果不是,继续向后扫描。
时间复杂度O(n^2) 空间复杂度O(n^2)
var longestPalindrome = function(s) {
let len = s.length
if (len === 1 || len === 0) {
return s
}
let dp = new Array, maxLen = 1, begin = 0
// dp定义为二维数组
for (let i = 0; i < len; i++) {
dp.push(new Array)
}
// dp[i][j] 表示 s[i..j] 是否是回文串,1为真,0为假
for (let i = 0; i < len; i++) {
for (let j = 0; j < len; j++) {
if (i === j) {
dp[i][i] = 1
}else {
dp[i][j] = 0
}
}
}
for (let j = 0; j < len; j++) {
for (let i = 0; i < j; i++) {
if (s[i] === s[j] && (i + 1 === j || dp[i+1][j-1])) {
dp[i][j] = 1
}
if (dp[i][j] && (j - i + 1 > maxLen)) {
maxLen = j - i + 1
begin = i
}
}
}
return s.substr(begin, maxLen)
};解题思想2:中心扩散,遍历所有的回文中心并尝试扩散,直到无法扩散为止,此时的回文串长度即为此回文中心下的最长回文串长度。然后对所有的长度求出最大值。
时间复杂度O(n^2) 空间复杂度O(1)
var longestPalindrome = function(s) {
let len = s.length
if (len <= 1) {
return s
}
let maxLen = 0, begin = 0
for (let i = 0; i < len; i++) {
let curMaxLen = Math.max(getPalindromeLength(s, i, i), getPalindromeLength(s, i, i + 1))
if (curMaxLen > maxLen) {
maxLen = curMaxLen
begin = i - parseInt((curMaxLen + 1) / 2) + 1
}
}
return s.substring(begin, begin + maxLen)
}
/**以中心点向两边扩散找到最长回文串的长度 */
/**
* @param {string} s
* @param {number} left 左索引
* @param {number} right 右索引
*/
function getPalindromeLength(s, left, right) {
// 如果在有效边界内并且左下标字符等于右下标字符
while (left >= 0 && right < s.length && s.charAt(left) === s.charAt(right)) {
left--
right++
}
return right - left - 1
}7. 整数反转
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1:输入:x = 123,输出:321
示例 2:输入:x = -123,输出:-321
示例 3:输入:x = 120,输出:21
示例 4:输入:x = 0,输出:0
提示:-2^31 <= x <= 2^31 - 1
/**
* @param {number} x
* @return {number}
*/
var reverse = function(x) {
let res = 0
while(x) {
res = res * 10 + x % 10;
if(res > Math.pow(2, 31) - 1 || res < Math.pow(-2, 31)) return 0;
x = ~~(x / 10);
}
return res
};
var reverse = function(x) {
let flag = x < 0 ? -1 : 1
let y = Math.abs(x)
let res = 0
while (y) {
res = res * 10 + y % 10
y = Math.floor(y / 10)
}
res = res * flag
return res > Math.pow(2, 31) - 1 || res < Math.pow(-2, 31) ? 0 : res
};8. 字符串转换整数
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
读入字符串并丢弃无用的前导空格
检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。
读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
将前面步骤读入的这些数字转换为整数(即,”123” -> 123, “0032” -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始)。
如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −231 的整数应该被固定为 −231 ,大于 231 − 1 的整数应该被固定为 231 − 1 。
返回整数作为最终结果。
注意:本题中的空白字符只包括空格字符 ‘ ‘ 。除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。
解题思想1:运用js的parseInt方法
/**
* @param {string} s
* @return {number}
*/
var myAtoi = function(s) {
//将字符串解析为十进制的整数。
const number = parseInt(s, 10);
//如果是NaN,则说明无法正常转换
if(isNaN(number)) {
return 0;
} else if (number < Math.pow(-2, 31) || number > Math.pow(2, 31) - 1) {
return number < Math.pow(-2, 31) ? Math.pow(-2, 31) : Math.pow(2, 31) - 1;
} else {
return number;
}
};解题思想2:
1.循环筛掉前置的空格;
2.判断符号位,如果符号位超过一个则不合法,直接返回0;
3.最后遍历所有数字位,把符号位和数字结合;
4.限制范围在-2^31到2^31-1之间;
var myAtoi = function(s) {
let sign = "",num = "",i = 0
// 处理前导空格
while(s[i] === " "){
i++;
}
// 判断符号位,如果符号位超过一个则不合法,直接返回0
while(s[i] === "+" || s[i] === "-"){
if(sign){
return 0;
}
sign = s[i++];
}
// 如果字符是数字并且处于字符串范围内
while(s[i] && s[i].charCodeAt() >= 48 && s[i].charCodeAt() <= 57){
num += s[i++];
}
// 把符号位和数字结合转换成数字
let res = Number(sign + num) || 0;
if (res < Math.pow(-2, 31) || res > Math.pow(2, 31) - 1) {
return res < Math.pow(-2, 31) ? Math.pow(-2, 31) : Math.pow(2, 31) - 1;
} else {
return res;
}
};解题思想3:不使用Number方法
var myAtoi = function(s) {
// 符号,1代表正数,-1代表负数
let sign = 1, res = 0, i = 0
// 处理前导空格
while(s[i] === " "){
i++
}
// 判断是否存在-字符
if (s[i] === '-') {
sign = -1
}
if (s[i] === '+' || s[i] === '-') {
i++
}
// 如果字符是数字并且处于字符串范围内
while(i < s.length && s[i].charCodeAt() >= 48 && s[i].charCodeAt() <= 57){
res = res * 10 + (s.charAt(i++) - '0')
}
// 如果是负数
if (sign === -1) {
res = -res
}
if (res < Math.pow(-2, 31) || res > Math.pow(2, 31) - 1) {
return res < Math.pow(-2, 31) ? Math.pow(-2, 31) : Math.pow(2, 31) - 1
} else {
return res
}
};11. 盛最多水的容器
给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。
示例1:输入:[1,8,6,2,5,4,8,3,7],输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:输入:height = [1,1],输出:1
示例 3:输入:height = [4,3,2,1,4],输出:16
解题思想1:两条线较短的那条是容器高度,两条线之间的距离是容器宽度,求最大的面积。时间复杂度O(n^2) 空间复杂度O(1)
/**
* @param {number[]} height
* @return {number}
*/
var maxArea = function(height) {
// 结果
let res = 0
// 数组长度
let n = height.length
for (let i = 0; i < n; i++) {
for (let j = i + 1; j < n; j++) {
// 两个条垂直线之间的面积(高度为较短的那条垂直线)
let area = (j - i) * Math.min(height[i], height[j])
// 面积最大的区域
res = Math.max(res, area)
}
}
return res
};解题思想2:双指针解法,时间复杂度O(n) 空间复杂度O(1)
var maxArea = function(height) {
// 结果
let res = 0
// 左指针
let left = 0
// 右指针
let right = height.length - 1
while (left < right) {
// 两个条垂直线之间的面积(高度为较短的那条垂直线)
let area = (right - left) * Math.min(height[right], height[left])
// 面积最大的区域
res = Math.max(res, area)
// 移动高度较短的线
if (height[left] < height[right]) {
left++
}else {
right--
}
}
return res
};14.最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 “”。
示例 1:输入:strs = [“flower”,”flow”,”flight”],输出:”fl”
示例 2:输入:strs = [“dog”,”racecar”,”car”],输出:””
解释:输入不存在公共前缀。
/**
* @param {string[]} strs
* @return {string}
*/
var longestCommonPrefix = function(strs) {
if (strs.length === 0) {
return '';
}
if (strs.length === 1) {
return strs[0];
}
let first = strs[0];
// 最后一个相同的char的index
let lastIndex = first.length - 1;
for (let i = 0; i < strs.length; i++) {
// 当前字符串
let cur = strs[i];
lastIndex = Math.min(cur.length - 1, lastIndex);
for (let j = 0; j <= lastIndex; j++) {
if (cur[j] !== first[j]) {
if (j === 0) {
return '';
} else {
lastIndex = j - 1;
break;
}
}
}
}
return first.substring(0, lastIndex + 1);
};17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按任意顺序返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例 1:
输入:digits = “23”
输出:[“ad”,”ae”,”af”,”bd”,”be”,”bf”,”cd”,”ce”,”cf”]
示例 2:输入:digits = “”,输出:[]
示例 3:输入:digits = “2”,输出:[“a”,”b”,”c”]
/**
* @param {string} digits
* @return {string[]}
*/
/**17. 电话号码的字母组合 */
var letterCombinations = function(digits) {
// 结果集
let res = []
if (digits.length === 0) {
return res
}
// 保存数字与字母的映射关系
let letterMap = new Map()
letterMap.set("2", "abc")
letterMap.set("3", "def")
letterMap.set("4", "ghi")
letterMap.set("5", "jkl")
letterMap.set("6", "mno")
letterMap.set("7", "pqrs")
letterMap.set("8", "tuv")
letterMap.set("9", "wxyz")
let combination = new String()
backTracking(res, letterMap, 0, digits, combination)
return res
};
/**
* @param {string[]} res 映射关系
* @param {Map} letterMap 映射关系
* @param {string} digits
* @param {number} index 当前项索引
* @param {string} combination 组合字符串
*
*/
function backTracking(res, letterMap, index, digits, combination) {
// 终止条件,当前项索引等于digits字符串长度
if (index === digits.length) {
res.push(combination.slice())
return
}else {
// 当前数字元素
let ch = digits.charAt(index)
// 获取对应数字的字符组合
let letters = letterMap.get(ch)
let len = letters.length
for (let i = 0; i < len; i++) {
// 将字符添加进组合
combination = combination.concat(letters.charAt(i))
backTracking(res, letterMap, index + 1, digits, combination)
combination = combination.substring(0, combination.length - 1)
}
}
}19. 删除链表倒数第n个节点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
进阶:你能尝试使用一趟扫描实现吗?
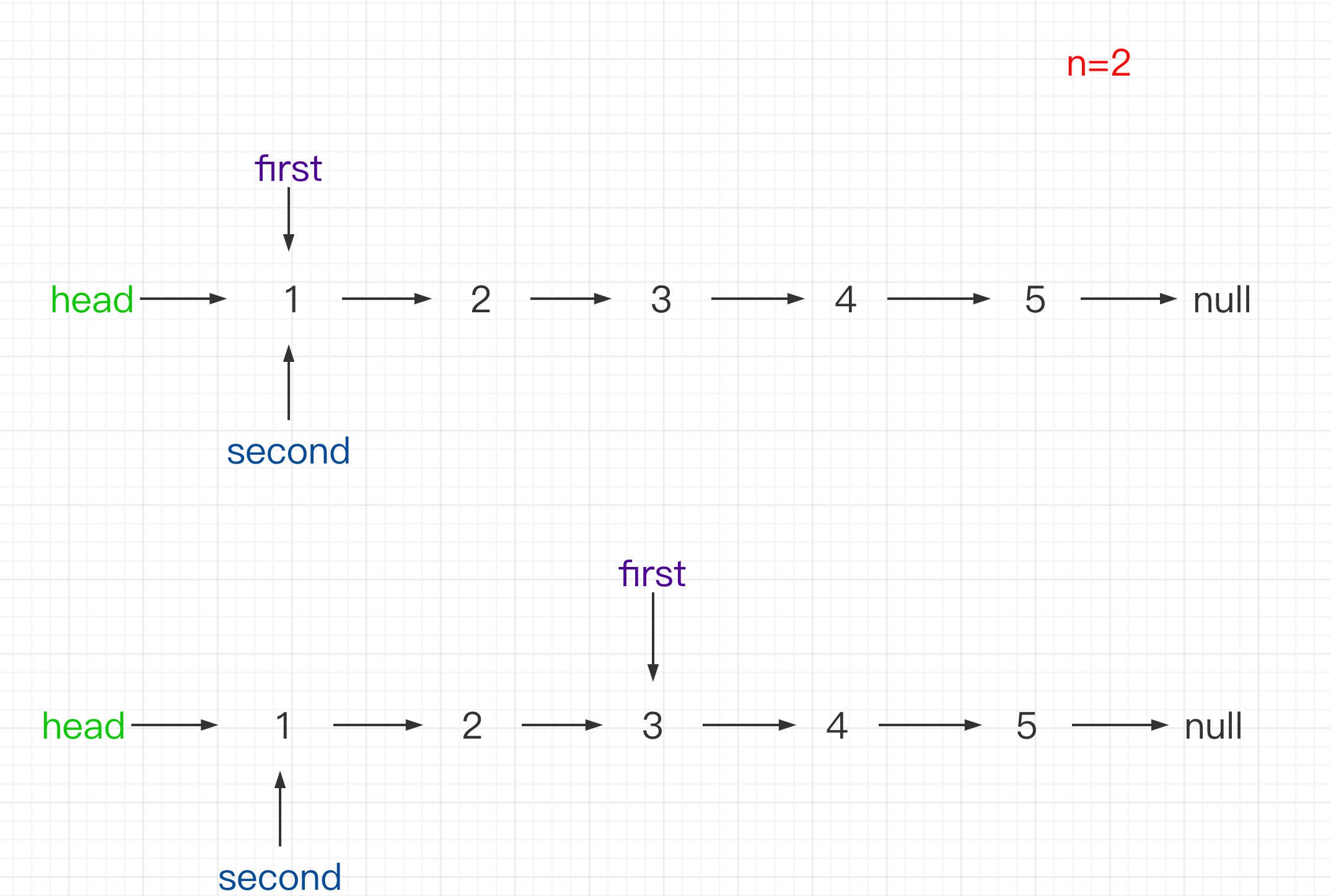
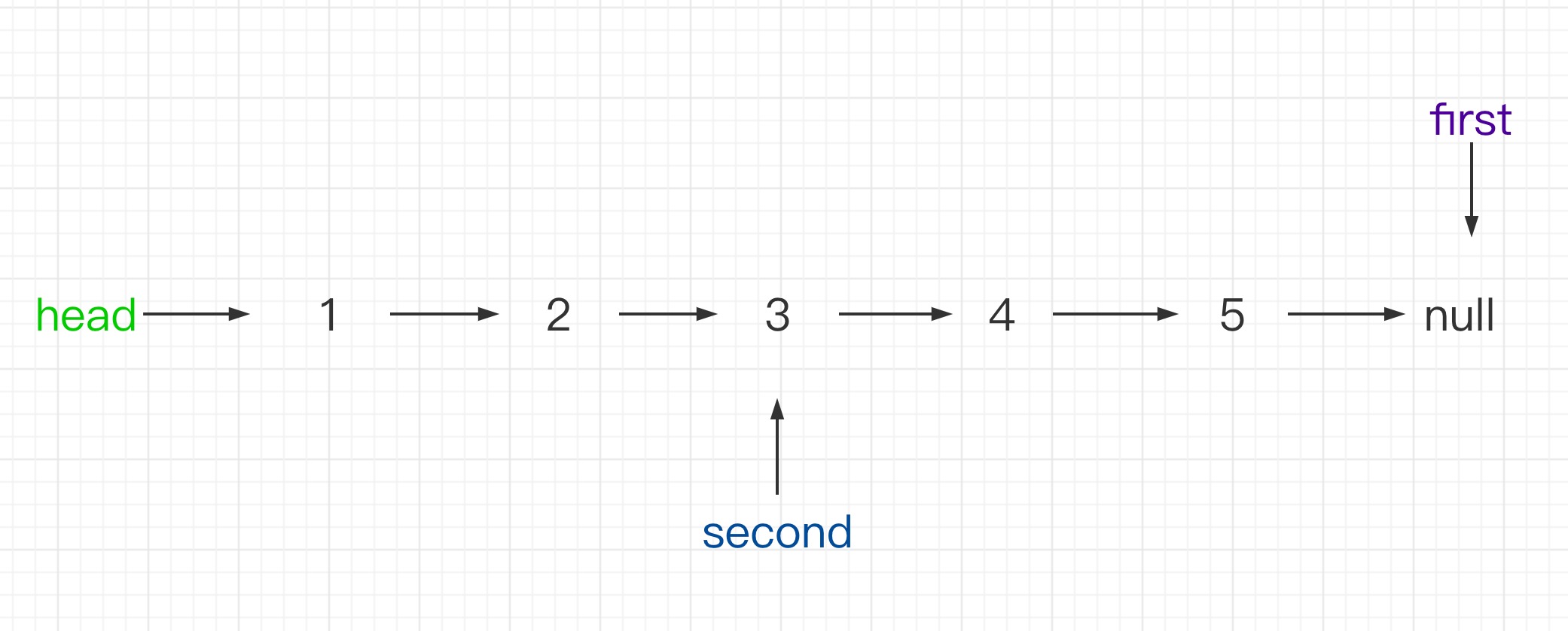
示例1:输入:head = [1,2,3,4,5], n = 2,输出:[1,2,3,5]
示例2:输入:head = [1], n = 1,输出:[]
示例3:输入:head = [1,2], n = 1,输出:[1]
解题思想1:快慢指针,要删除链表的节点,找到该节点的前驱节点。时间复杂度 O(n),空间复杂度 O(1)
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @param {number} n
* @return {ListNode}
*/
var removeNthFromEnd = function(head, n) {
if(head === null){
return head //如果head为空
}
let first = head //定义个快指针
let second = head //定义一个慢指针
while(n){
first = first.next //快指针前进n步
n--
}
if(first === null){
return head.next //如果此时快指针超过链表,说明头节点就是倒数第n个节点,考虑删除头节点的情况
}
while(first.next !== null){
first = first.next //两指针一起遍历移动,直到快指针指向最后一个节点,慢指针指向倒数第n+1个节点
second = second.next
}
second.next = second.next.next //删除倒数第n个节点
return head
};解题思想2:暴力求解,找到列表的长度length,删除从列表头部开始的第L-n+1个节点。时间复杂度 O(n),空间复杂度 O(1)
var removeNthFromEnd = function(head, n) {
let length = 0 //链表长度
let res = head
while(head){
head = head.next //获取链表长度
length++
}
head = res //重新赋值
let count = length- n//要删除的节点
// 如果是正向第一个结点,则头结点被删除,只需要直接返回头结点的next
if (count === 0) {
return head.next;
}
for(let i = 0; i < count - 1; i++){
head = head.next //直接遍历到该结点的前一个结点
}
head.next = head.next.next
return res
};15. 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:输入:nums = [-1,0,1,2,-1,-4],输出:[[-1,-1,2],[-1,0,1]]
示例 2:输入:nums = [],输出:[]
示例 3:输入:nums = [0],输出:[]
解题思想:
1.给数组排序,避免重复数组
2.遍历数组,从0遍历到length-2(防止下标越界)
3.如果当前的数字等于前一个数字,则跳过这个数(去重)
4.如果数字不同,则设置start=i+1,end = length - 1,查看i,start,end三者之和比大还是小,如果比0小,start++,如果比0大,end–,如果等于0,将他们加入结果数组中
5.返回结果
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function(nums) {
// 结果集
let res = [];
// 为数组排序
nums.sort((pre, next) => {
return pre - next;
})
console.log('排序', nums)
for (let i = 0; i < nums.length - 2; i++) {
// 如果是第一个数并且前一个数不等于当前数
if (i === 0 || nums[i] !== nums[i-1]) {
let start = i + 1, end = nums.length - 1;
while (start < end) {
let sum = nums[i] + nums[start] + nums[end]
if (sum === 0) {
res.push([nums[i], nums[start], nums[end]]);
start++;
end--;
// 去重
while (start < end && nums[start] === nums[start-1]) {
start++;
}
while (start < end && nums[end] === nums[end+1]) {
end--;
}
} else if (sum < 0) {
start++;
} else {
end--;
}
}
}
}
return res;
};20. 有效的括号
给定一个只包括 ‘(‘,’)’,’{‘,’}’,’[‘,’]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
示例 1:输入:s = “()”,输出:true
示例 2:输入:s = “()[]{}”,输出:true
示例 3:输入:s = “(]”,输出:false
示例 4:输入:s = “([)]”,输出:false
解题思想:通过栈来解决
/**
* @param {string} s
* @return {boolean}
*/
var isValid = function(s) {
let stack = [];
for (let i = 0; i < s.length; i++) {
if (s[i] === '(') {
stack.push(')');
} else if (s[i] === '[') {
stack.push(']');
} else if (s[i] === '{') {
stack.push('}');
} else {
if (stack.length === 0) {
return false;
}
if (stack.pop() != s[i]) {
return false;
}
}
}
return stack.length === 0;
};21. 合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例1:输入:l1 = [1,2,4], l2 = [1,3,4],输出:[1,1,2,3,4,4]
示例2:输入:l1 = [], l2 = [],输出:[]
示例3:输入:l1 = [], l2 = [0],输出:[0]
解决思想:判断两个链表当前节点值的大小,进行比较,然后节点更新遍历。
迭代法:时间复杂度O(n)空间复杂度O(n)
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} l1
* @param {ListNode} l2
* @return {ListNode}
*/
var mergeTwoLists = function(l1, l2) {
let res = new ListNode()
let cur = res
while(l1 && l2){
if(l1.val <= l2.val){
cur.next = l1 //如果l1的val小,将cur的next指向l1当前节点,然后l1向后遍历
l1 = l1.next
}else {
cur.next = l2
l2 = l2.next
}
cur = cur.next // cur继续更新
}
if(l1 === null){
cur.next = l2
}
if(l2 === null){
cur.next = l1
}
return res.next
};递归法
var mergeTwoLists = function(l1, l2) {
if(l1 === null || l2 === null){
return l1 || l2
}
if(l1.val <= l2.val){
l1.next = mergeTwoLists(l1.next,l2)
return l1
}else{
l2.next = mergeTwoLists(l1,l2.next)
return l2
}
};22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且有效的括号组合。
示例 1:
输入:n = 3
输出:[“((()))”,”(()())”,”(())()”,”()(())”,”()()()”]
示例 2:输入:n = 1,输出:[“()”]
解题思想:括号有效:左边的括号数大于或等于右边括号数
/**
* @param {number} n
* @return {string[]}
*/
var generateParenthesis = function(n) {
// 结果集
let res = []
if (n === 0) {
return res
}
// 组合集
let combination = new String()
backTracking(n, res, 0, 0, combination)
return res
};
/**
* @param {number} n
* @param {string[]} res
* @param {number} left 左边括号数量
* @param {number} right 右边括号数量
* @param {string[]} combination 当前获取到的括号的样子/组合集
*/
function backTracking(n, res, left, right, combination) {
// 不是有效的括号
if (right > left) {
return
}
// 终止条件,当左边括号数等于右边括号数并且等于n时
if (left === n && right === n) {
// 加入括号组合
res.push(combination.slice())
return
}
// 加左括号
if (left < n) {
backTracking(n, res, left + 1, right, combination + '(')
}
// 加右括号
if (right < left) {
backTracking(n, res, left, right + 1, combination + ')')
}
}24. 两两交换链表中的节点
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例1:输入:head = [1,2,3,4],输出:[2,1,4,3]
示例2:输入:head = [],输出:[]
示例3:输入:head = [1],输出:[1]
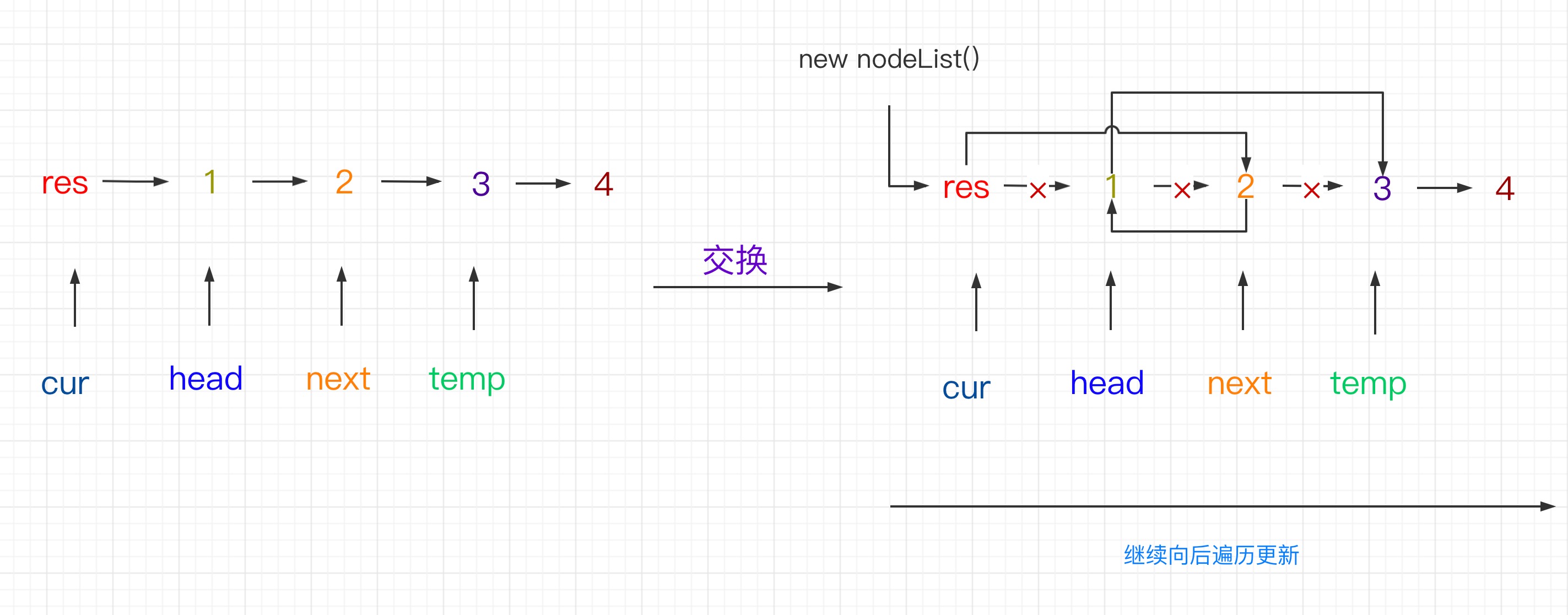
解题思想1:迭代法 时间复杂度O(n) 空间复杂度O(1)
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var swapPairs = function(head) {
if(head === null || head.next === null){
return head
}
let res = new ListNode() //定义一个新节点指向head
res.next = head
let cur = res
let next = null // 用于保存后续的两个节点
let temp = null
while(cur.next !== null && cur.next.next !== null){
next = head.next //节点赋值
temp = next.next
cur.next = next //交换节节点
next.next = head
head.next = temp
cur = head //继续遍历更新
head = head.next
}
return res.next
};解题思想2:递归法 时间复杂度O(n) 空间复杂度O(n)
var swapPairs = function(head) {
if(head === null || head.next === null){
return head //如果头节点为空或者只有一个节点就返回头节点
}
let next = head.next //将头节点后一个节点进行赋值保存
head.next = swapPairs(head.next.next)
next.next = head
return next
}26. 删除有序数组中的重复项
给你一个有序数组 nums ,请你原地删除重复出现的元素,使每个元素只出现一次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
/**
* @param {number[]} nums
* @return {number}
*/
var removeDuplicates = function(nums) {
const n = nums.length;
if (n === 0) {
return 0;
}
// 快指针用来扫描,慢指针用来指向答案位置
let fast = 1, slow = 1;
while (fast < n) {
// 找到不重复项
if (nums[fast] !== nums[fast - 1]) {
// 慢指针覆盖元素
nums[slow] = nums[fast];
++slow;
}
++fast;
}
return slow;
};27. 移除元素
给你一个数组 nums 和一个值 val,你需要原地移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
/**
* @param {number[]} nums
* @param {number} val
* @return {number}
*/
var removeElement = function(nums, val) {
const n = nums.length;
let left = 0;
for (let right = 0; right < n; right++) {
if (nums[right] !== val) {
nums[left] = nums[right];
left++;
}
}
return left;
};34. 在排序数组中查找元素的第一个和最后一个位置
解题思想1: 直接遍历,时间复杂度O(n) 空间复杂度O(1)
/**
* @param {number[]} nums
* @param {number} target
* @return {number[]}
*/
var searchRange = function(nums, target) {
let res = []
return [indexOf(nums, target), lastIndexOf(nums, target)]
};
function indexOf(nums, target) {
for (let i = 0; i < nums.length; i++) {
if (nums[i] === target) {
return i
}
}
return -1
}
function lastIndexOf(nums, target) {
for (let i = nums.length - 1; i >= 0; i--) {
if (nums[i] === target) {
return i
}
}
return -1
}解题思想2:二分查找,时间复杂度O(logn) 空间复杂度O(1)
var searchRange = function(nums, target) {
let len = nums.length
if (len === 0) {
return [-1, -1]
}
let firstIndex = indexOf(nums, target)
if (firstIndex === -1) {
return [-1, -1]
}
let lastIndex = lastIndexOf(nums, target)
return [firstIndex, lastIndex]
};
// 第一个位置
function indexOf(nums, target) {
let left = 0
let right = nums.length - 1
while (left < right) {
let mid = Math.floor((left + right) / 2)
if (nums[mid] < target) {
left = mid + 1
} else if (nums[mid] > target) {
right = mid - 1
} else {
right = mid
}
}
if (nums[left] === target) {
return left
}
return -1
}
// 最后一个位置
function lastIndexOf(nums, target) {
let left = 0
let right = nums.length - 1
while (left < right) {
// +1防止陷入死循环
let mid = Math.floor((left + right + 1) / 2)
if (nums[mid] < target) {
left = mid + 1
} else if (nums[mid] > target) {
right = mid - 1
} else {
left = mid
}
}
return left
}
const binarySearch = (nums, target, lower) => {
let left = 0, right = nums.length - 1, ans = nums.length;
while (left <= right) {
const mid = Math.floor((left + right) / 2);
if (nums[mid] > target || (lower && nums[mid] >= target)) {
right = mid - 1;
ans = mid;
} else {
left = mid + 1;
}
}
return ans;
}
var searchRange = function(nums, target) {
let ans = [-1, -1];
const leftIdx = binarySearch(nums, target, true);
const rightIdx = binarySearch(nums, target, false) - 1;
if (leftIdx <= rightIdx && rightIdx < nums.length && nums[leftIdx] === target && nums[rightIdx] === target) {
ans = [leftIdx, rightIdx];
}
return ans;
};39. 组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
说明:所有数字(包括 target)都是正整数。解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7,
所求解集为:
[[7],[2,2,3]]
示例 2:
输入:candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
/**
* @param {number[]} candidates
* @param {number} target
* @return {number[][]}
*/
/**39. 组合总和 */
var combinationSum = function(candidates, target) {
// 结果集
let res = []
// 每一层结果
let combineList = []
dfs(0, combineList, res, candidates, target)
return res
};
/**
* @param {number} start 起始指针
* @param {number[]} combineList 每一层结果
* @param {number[]} res 结果
* @param {number[]} candidates
* @param {number} target
*/
function dfs(start, combineList, res, candidates, target) {
// 终止条件,集合找到了
if (target === 0) {
// 拷贝一份结果
res.push(combineList.slice())
return
}
for (let i = start; i < candidates.length; i++) {
// 小于等于情况下可以找组合
if (candidates[i] <= target) {
combineList.push(candidates[i])
// 元素可以重复选择,下次的循环可以从自身开始
dfs(i, combineList, res, candidates, target - candidates[i])
combineList.pop()
}
}
}45. 跳跃游戏 II
给你一个非负整数数组 nums ,你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。你的目标是使用最少的跳跃次数到达数组的最后一个位置。假设你总是可以到达数组的最后一个位置。
示例 1:输入: nums = [2,3,1,1,4],输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:输入: nums = [2,3,0,1,4],输出: 2
/**
* @param {number[]} nums
* @return {number}
*/
var jump = function(nums) {
// 下一步所能覆盖的最远下标
let newMax = 0;
// 当前步数所能到达的最远下标
let maxi = 0;
// 总共跳跃的次数
let step = 0;
for (let i = 0; i < nums.length - 1; i++) {
let num = nums[i];
// 找到下一步所能覆盖的最远下标
newMax = Math.max(newMax, num + i);
// 当等于当前步数的限制值时
if (i === maxi) {
step++;
maxi = newMax;
// 当最远下标大于数组长度时,跳出
if (maxi >= nums.length - 1) {
break;
}
}
}
return step;
};46. 全排列
给定一个不含重复数字的数组 nums ,返回其所有可能的全排列。你可以按任意顺序返回答案。
示例1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例2:输入:nums = [0,1],输出:[[0,1],[1,0]]
示例3:输入:nums = [1],输出:[[1]]
解题思想:按顺序枚举每个位置可能出现的数字,之前已经出现的数字在接下来选择的数字中不能出现。树形结构。
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permute = function(nums) {
// 数组长度
let len = nums.length
// 返回结果
let res = []
// 如果数组长度为0
if (len === 0) {
return res
}
// 排列路径
let path = []
// 元素是否使用过
let used = new Boolean(len)
dfs(nums, len, 0, path, used, res)
return res
};
/**
* @param {number[]} nums 数组
* @param {number} len 数组长度
* @param {number} depth 当前层
* @param {number[]} path 数组排列
* @param {boolean} used 元素是否被使用过
* @param {number[]} res 返回结果
*/
function dfs(nums, len, depth, path, used, res) {
// 当前层等于数组长度,递归终止条件
if (depth === len) {
// 添加排列,拷贝一份path
res.push(path.slice())
return
}
for (let i = 0; i < len; i++) {
// 如果元素已经被使用了
if (used[i]) {
continue
}
// 加入排列
path.push(nums[i])
// 元素被使用赋值true
used[i] = true
// 下一层
dfs(nums, len, depth + 1, path, used, res)
// 回溯
path.pop()
used[i] = false
}
}47. 全排列 ||
给定一个可包含重复数字的序列 nums ,按任意顺序返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],[1,2,1],[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permuteUnique = function(nums) {
// 结果集
let res = []
// 数组长度
let len = nums.length
// 排列
let path = []
if (len === 0) {
return res
}
// 是否使用过元素
let used = new Boolean(len)
// 将元素排序,方便后续去重
nums.sort()
dfs(nums, path, 0, len, used, res)
return res
};
/**
* @param {number[]} nums 数组
* @param {number} len 数组长度
* @param {number} depth 当前层
* @param {number[]} path 数组排列
* @param {boolean} used 元素是否被使用过
* @param {number[]} res 返回结果
*/
function dfs(nums, path, depth, len, used, res) {
if (depth === len) {
res.push(path.slice())
return
}
for (let i = 0; i < len; i++) {
if (used[i]) {
continue
}
// 如果当前元素与前一个元素相等并且前一个元素被使用过,去重
if (i > 0 && nums[i] === nums[i - 1] && used[i - 1]) {
continue
}
path.push(nums[i])
used[i] = true
dfs(nums, path, depth + 1, len, used, res)
path.pop()
used[i] = false
}
}48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
解题思想1:对于矩阵中第 i 行的第 j 个元素,在旋转后,它出现在倒数第 i 列的第 j 个位置。
时间复杂度O(n^2) 空间复杂度O(n^2)
/**
* @param {number[][]} matrix
* @return {void} Do not return anything, modify matrix in-place instead.
*/
var rotate = function(matrix) {
let n = matrix.length;
let matrixTemp = new Array()
// 定义matrixTemp为二维数组
for (let i = 0; i < n; i++) {
matrixTemp.push(new Array())
}
for (let i = 0; i < n; i++) {
matrixTemp[i].push(new Array())
}
// let matrixTemp = new Array(n).fill(0).map(() => new Array(n).fill(0));
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
matrixTemp[j][n - i - 1] = matrix[i][j]
}
}
// 重新赋值
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
matrix[i][j] = matrixTemp[i][j]
}
}
}解题思想2:原地旋转,时间复杂度O(n) 空间复杂度O(1)。
var rotate = function(matrix) {
// 数组长度
let n = matrix.length
for (let i = 0; i < Math.floor(n / 2); i++) {
// 内圈
for (let j = i; j < n - i - 1; j++) {
// 交换
let temp = matrix[i][j]
matrix[i][j] = matrix[n-j-1][i]
matrix[n-j-1][i] = matrix[n-i-1][n-j-1]
matrix[n-i-1][n-j-1] = matrix[j][n-i-1]
matrix[j][n-i-1] = temp
}
}
};50. Pow(x, n)
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,x^n)。
示例 1:输入:x = 2.00000, n = 10,输出:1024.00000
示例 2:输入:x = 2.10000, n = 3,输出:9.26100
示例 3:输入:x = 2.00000, n = -2,输出:0.25000
解释:2-2 = 1/2^2 = 1/4 = 0.25
/**
* @param {number} x
* @param {number} n
* @return {number}
*/
var myPow = function(x, n) {
if (n < 0) {
return 1 / myPowHelp(x, Math.abs(n));
}
return myPowHelp(x, n);
};
function myPowHelp(x, n) {
let res = 1;
let temp = x;
// 对n进行二进制的拆分
while (n > 0) {
if (n % 2 === 1) {
// 如果n二进制表示的最低位为1,需要计入
res = res * temp;
}
temp *= temp;
// 舍弃n二进制表示的最低位,这样每次只要判断最低位即可
n = Math.floor(n / 2);
}
return res;
}51. 翻转字符串里的单词
给你一个字符串 s ,逐个翻转字符串中的所有单词。单词是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的单词分隔开。请你返回一个翻转 s 中单词顺序并用单个空格相连的字符串。
说明:输入字符串 s 可以在前面、后面或者单词间包含多余的空格。翻转后单词间应当仅用一个空格分隔。翻转后的字符串中不应包含额外的空格。
示例 1:输入:s = “the sky is blue”,输出:”blue is sky the”
示例 2:输入:s = “ hello world “,输出:”world hello”
解释:输入字符串可以在前面或者后面包含多余的空格,但是翻转后的字符不能包括。
示例 3:输入:s = “a good example”,输出:”example good a”
解释:如果两个单词间有多余的空格,将翻转后单词间的空格减少到只含一个。
解题思想1:使用字符串、数组的方法。时间复杂度:O(n) 空间复杂度:O(n)
/**
* @param {string} s
* @return {string}
*/
var reverseWords = function(s) {
return s.trim().split(/\s+/).reverse().join(' ')
};解题思想2:反向遍历 时间复杂度:O(n) 空间复杂度:O(n)
var reverseWords = function(s) {
let arr = s.split(' ')
let res = ''
for (let i = arr.length - 1; i >= 0; i--) {
if (arr[i] === '') {
continue
}else {
res += arr[j] + ' '
}
}
return res.trim()
};解题思想3:双指针,从后往前遍历字符串;
1.右指针遇空格就跳过,直到单词末尾,将左指针指向右指针;
2.左指针继续向前,直到遇到空格或小于0才停下,此时左右指针中间的就是单词 ;
3.把右指针指向左指针,开始下一轮遍历;
4.如果还有新单词,就给上一个单词后面添加一个空格;
空间复杂度:O(1)
var reverseWords = function(s) {
let right= s.length - 1, left = right, res = '';
while (left >= 0) {
//先找到单词的尾部
while (s[right] === ' ') {
right--;
}
// 将左指针指向右指针
left = right;
//如果还有新单词,就给上一个单词后面添加一个空格
if (left >= 0 && res) {
res += " ";
}
//再找到单词的头部(左指针继续向前,直到遇到空格或小于0才停下,此时左右指针中间的就是单词)
while (s[left] && s[left] !== " ") {
left--;
}
//遍历单词并添加,
for (let i = left + 1, j = right; i <= j; i++) {
res += s[i];
}
//跳到下一个单词,把右指针指向左指针,开始下一轮遍历
right = left;
}
return res;
};53. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例 1:输入:nums = [-2,1,-3,4,-1,2,1,-5,4],输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:输入:nums = [1],输出:1
示例 3:输入:nums = [0],输出:0
解题思想1:暴力求解 时间复杂度O(n^2) 空间复杂度O(1)
var maxSubArray = function(nums) {
// res结果初始和数组下标为0的元素
let res = nums[0]
// 当前连续子数组之和
let temp = 0
for (let i = 0; i < nums.length; i++) {
temp = 0
for (let j = i; j < nums.length; j++) {
temp += nums[j]
res = Math.max(temp, res)
}
}
return res
};解题思想2:动态规划 时间复杂度O(n) 空间复杂度O(1)
var maxSubArray = function(nums) {
// res结果初始和数组下标为0的元素
let res = nums[0]
// 当前连续子数组最大和
let temp = 0
// 遍历数组
for (let value of nums) {
// 当前连续子数组之和与后续数组元素进行比较,取最大值
temp = Math.max(temp + value, value)
// 结果取最大值
res = Math.max(res, temp)
}
return res
};54. 螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
解题思想:如果数组为空,返回空数组;定义4个边界以及当前的方向;当左边界<=右边界并且上边界<=下边界时,执行while循环,按照右、下、左、上的顺序依次将路径上的元素添加到结果集中。
var spiralOrder = function(matrix) {
// 结果集
let res = []
// 如果数组为空
if (matrix.length === 0) {
return res
}
// 定义4个边界
let top = 0, bottom = matrix.length - 1, left = 0, right = matrix[0].length - 1
// 方向
const RIGHT = 'right', TOP = 'top', LEFT = 'left', DOWN = 'down'
let direction = RIGHT
while (top <= bottom && left <= right) {
// 方向为右时
if (direction === RIGHT) {
// 遍历此方向的元素
for (let i = left; i <= right; i++) {
// 加入结果集
res.push(matrix[top][i])
}
// 边界值更新
top++
// 修改方向
direction = DOWN
}else if (direction === DOWN) {
for (let i = top; i <= bottom; i++) {
res.push(matrix[i][right])
}
right--
direction = LEFT
}else if (direction === LEFT) {
for (let i = right; i >= left; i--) {
res.push(matrix[bottom][i])
}
bottom--
direction = TOP
}else if (direction === TOP) {
for (let i = bottom; i >= top; i--) {
res.push(matrix[i][left])
}
left++
direction = RIGHT
}
}
return res
};55. 跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标。
示例 1:输入:nums = [2,3,1,1,4],输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:输入:nums = [3,2,1,0,4],输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
/**
* @param {number[]} nums
* @return {boolean}
*/
var canJump = function(nums) {
// 保存每个位置可以到达的最远的位置
let jump = [];
for (let i = 0; i < nums.length; i++) {
// 初始化jump数组
jump.push(i + nums[i]);
}
// 当前所在位置
let index = 0;
// 当前可以到达的最远位置
let maxJump = jump[0];
while (index < jump.length && index <= maxJump) {
if (maxJump < jump[index]) {
maxJump = jump[index];
}
index++;
}
// 如果index等于数组长度
if (index === jump.length) {
return true;
}
return false;
};56. 合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
解题思想1:有重叠就合并
/**
* @param {number[][]} intervals
* @return {number[][]}
*/
var merge = function(intervals) {
// 结果
let res = []
let len = intervals.length
let i = 0
// 当前集合
let cur = []
// 为数组排序,区间左边界元素升序排列
intervals.sort((pre, next) => {
return pre[0] - next[0]
})
while (i < len) {
// 下一个集合
let next = intervals[i]
if (cur.length === 0) {
cur = next
} else {
// 如果能够合并
if (cur[1] >= next[0]) {
// 取两个区间右边界最大的一个
cur = [cur[0], Math.max(cur[1], next[1])]
} else {
res.push([...cur])
cur = next
}
}
i++
}
if (cur.length > 0) {
res.push([...cur])
}
return res
};解题思想2:找到一系列重叠区间之后再合并
var merge = function(intervals) {
let len = intervals.length
// 区间起点集合
let startArr = []
// 区间终点集合
let endArr = []
for (let i = 0; i < len; i++) {
console.log(intervals[i])
startArr.push(intervals[i][0])
endArr.push(intervals[i][1])
}
// 集合排序
startArr.sort((pre, next) => {
return pre - next
})
endArr.sort((pre, next) => {
return pre - next
})
// 结果
let res = []
// 一个全局起点
let start = 0
for (let i = 0; i < len; i++) {
if (i === len - 1 || startArr[i + 1] > endArr[i]) {
res.push([startArr[start], endArr[i]])
// 更新全局起点
start = i + 1
}
}
return res
}61 旋转链表
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置,k非负数。
示例1:输入:head = [1,2,3,4,5], k = 2,输出:[4,5,1,2,3]
示例2:输入:head = [0,1,2], k = 4,输出:[2,0,1]
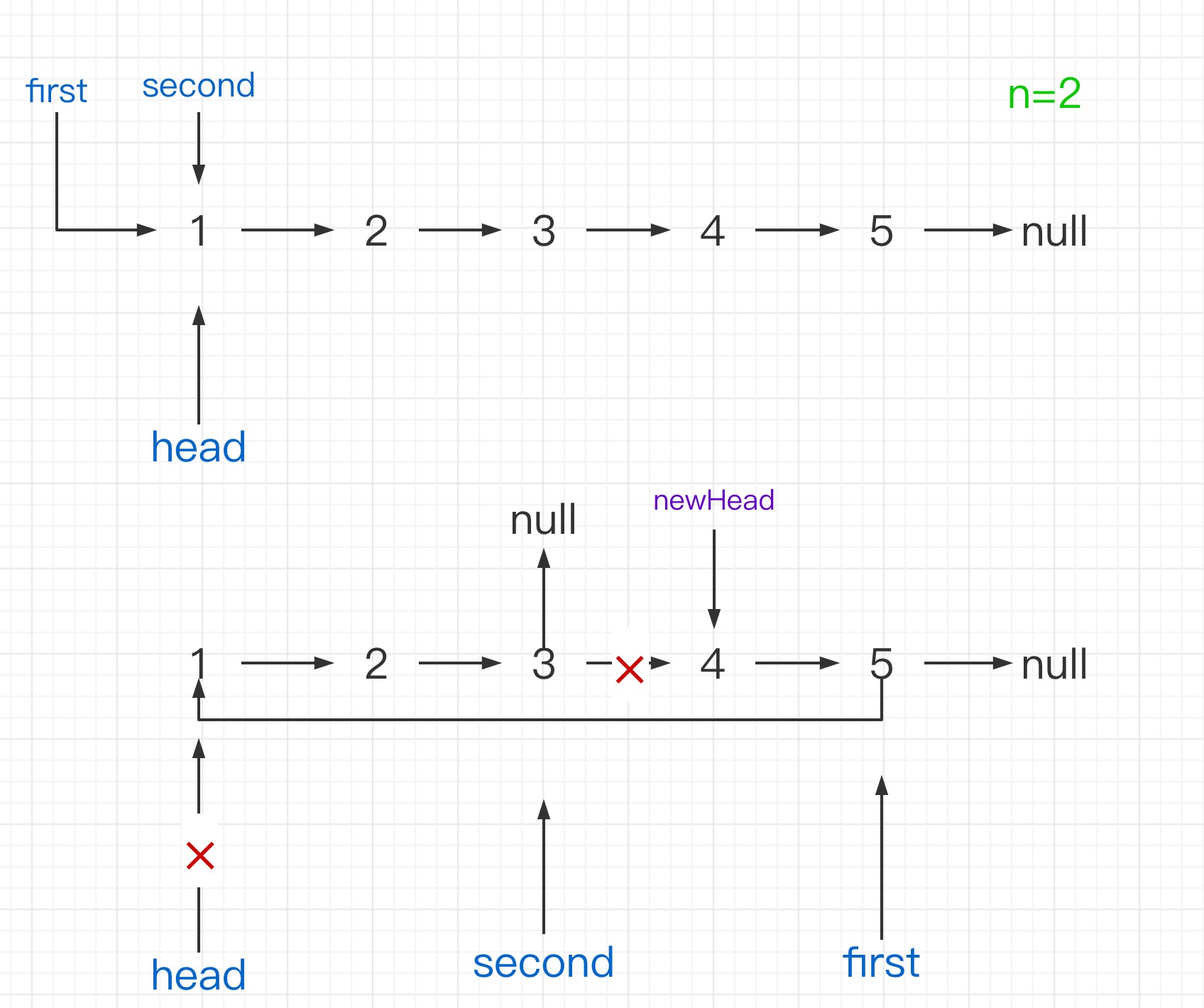
解题思想:找到倒数第k个节点放在链表最前面,利用快慢指针的方式。时间复杂度:O(N) 空间复杂度:O(1)
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @param {number} k
* @return {ListNode}
*/
var rotateRight = function(head, k) {
if(head === null){
return head
}
let cur = head
let first = head //快指针
let second = head //慢指针
let length = 0 //链表长度
while(cur !== null){
length++ //获取链表长度
cur = cur.next
}
k = k % length //可能会有k大于长度的情况
if(k === 0){
return head
}
for(let i = 0; i < k; i++){
first = first.next
}
while(first.next !== null){
first = first.next
second = second.next //找到慢指针需要断链的节点
}
let newHead = second.next
second.next = null
first.next = head
return newHead
};62. 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(标记为 “Finish” )。问总共有多少条不同的路径?
示例1:输入:m = 3, n = 7,输出:28
示例 2:输入:m = 3, n = 2,输出:3
解释:从左上角开始,总共有 3 条路径可以到达右下角。
1.向右 -> 向下 -> 向下
2.向下 -> 向下 -> 向右
3.向下 -> 向右 -> 向下
/**
* @param {number} m
* @param {number} n
* @return {number}
*/
var uniquePaths = function(m, n) {
let memo = [];
for (let i = 0; i < n; i++) {
memo.push(new Array());
}
for (let row = 0; row < n; row++) {
memo[row][0] = 1;
}
for (let col = 0; col < m; col++) {
memo[0][col] = 1;
}
for (let i = 1; i < n; i++) {
for (let j = 1; j < m; j++) {
memo[i][j] = memo[i-1][j] + memo[i][j-1];
}
}
return memo[n-1][m-1];
};64. 最小路径和
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:每次只能向下或者向右移动一步。
示例1:输入:grid = [[1,3,1],[1,5,1],[4,2,1]],输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:输入:grid = [[1,2,3],[4,5,6]],输出:12
解题思想:动态规划:状态设置,令dp[i][j]表示从(i, j)点走到(m-1,n-1)点的最小路径和,状态转移方程,由于每次只能往右走或者往下走,所以从(i,j)只能走到(i+1, j)或者(i,j+1)。dp[i][j]的前继状态只有dp[i+1][j],dp[i][j+1],所以在两者取最小,然后加上这个格子的数值就行啦
var minPathSum = function(grid) {
if (grid == null || grid.length == 0 || grid[0].length == 0) {
return 0;
}
let rows = grid.length, columns = grid[0].length;
// 状态转移方程,二维数组,dp[i][j]表示从(i, j)点走到(m-1,n-1)点的最小路径和
let dp = [];
for (let i = 0; i < rows; i++) {
dp[i] = new Array()
// dp为二维数组
for (let j = 0; j < columns; j++) {
dp[i][j] = new Array()
}
}
dp[0][0] = grid[0][0];
for (let i = 1; i < rows; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (let j = 1; j < columns; j++) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
}
for (let i = 1; i < rows; i++) {
for (let j = 1; j < columns; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[rows - 1][columns - 1];
};67. 二进制求和
给你两个二进制字符串,返回它们的和(用二进制表示)。输入为 非空 字符串且只包含数字 1 和 0。
示例 1:输入: a = “11”, b = “1”,输出: “100”
示例 2:输入: a = “1010”, b = “1011”,输出: “10101”
/**
* @param {string} a
* @param {string} b
* @return {string}
*/
var addBinary = function(a, b) {
let n1 = a.length - 1;
let n2 = b.length - 1;
// 进位,结果
let cur = 0, res = '';
while (n1 >= 0 && n2 >= 0) {
// 求和
let sum = (a[n1] - '0') + (b[n2] - '0') + cur;
cur = Math.floor(sum / 2);
sum = sum % 2;
res += sum;
n1--;
n2--;
}
while (n1 >= 0) {
// 求和
let sum = (a[n1] - '0') + cur;
cur = Math.floor(sum / 2);
sum = sum % 2;
res += sum;
n1--;
}
while (n2 >= 0) {
// 求和
let sum = (b[n2] - '0') + cur;
cur = Math.floor(sum / 2);
sum = sum % 2;
res += sum;
n2--;
}
// 如果还存在进位
if (cur > 0) {
res += cur;
}
return res.split('').reverse().join('');
};82 删除排序链表中的重复元素II
存在一个按升序排列的链表,给你这个链表的头节点 head ,请你删除链表中所有存在数字重复情况的节点,只保留原始链表中没有重复出现的数字。返回同样按升序排列的结果链表。
示例1:输入:head = [1,2,3,3,4,4,5],输出:[1,2,5]
示例2:输入:head = [1,1,1,2,3],输出:[2,3]
解题思想:如下图
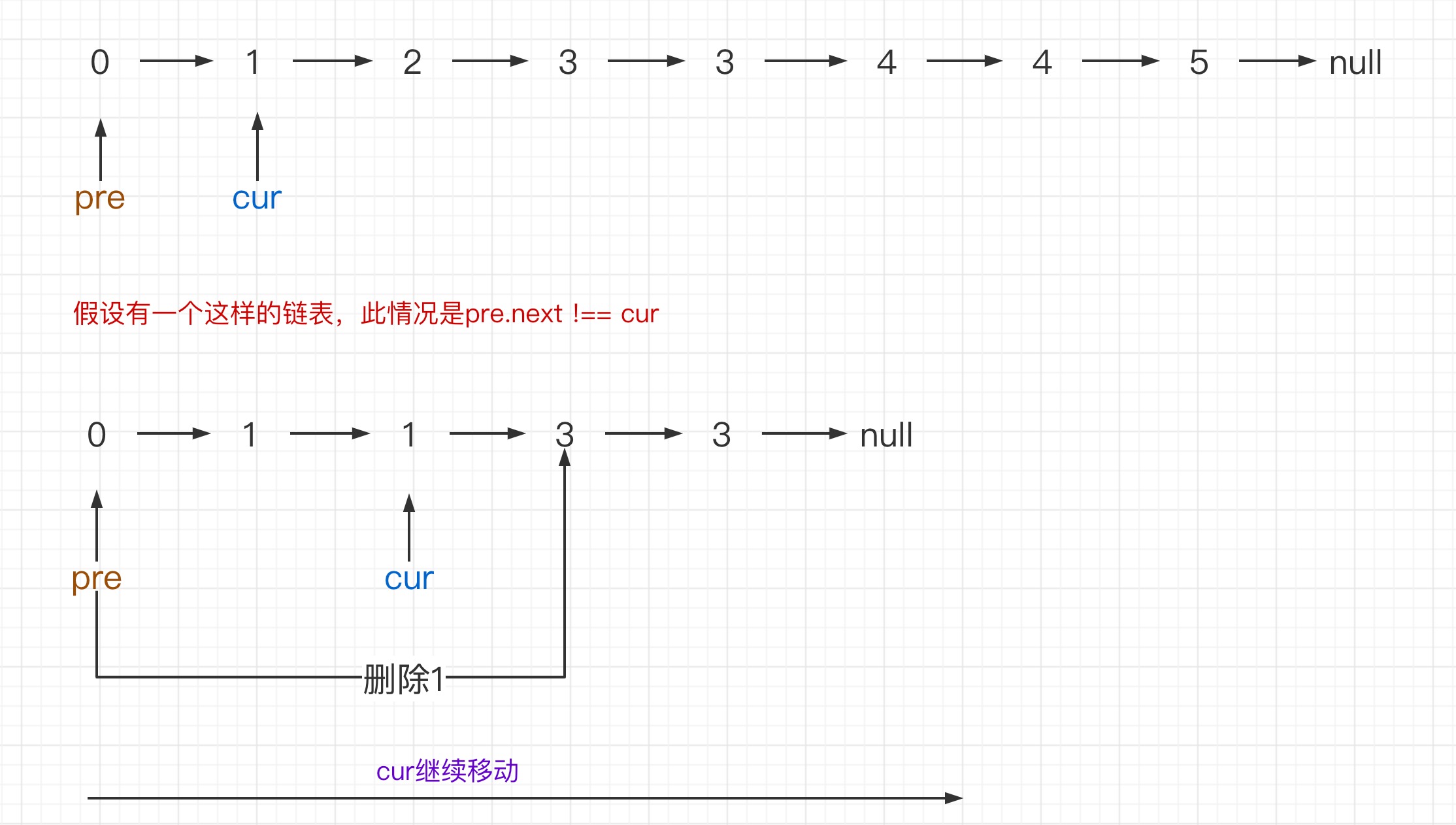
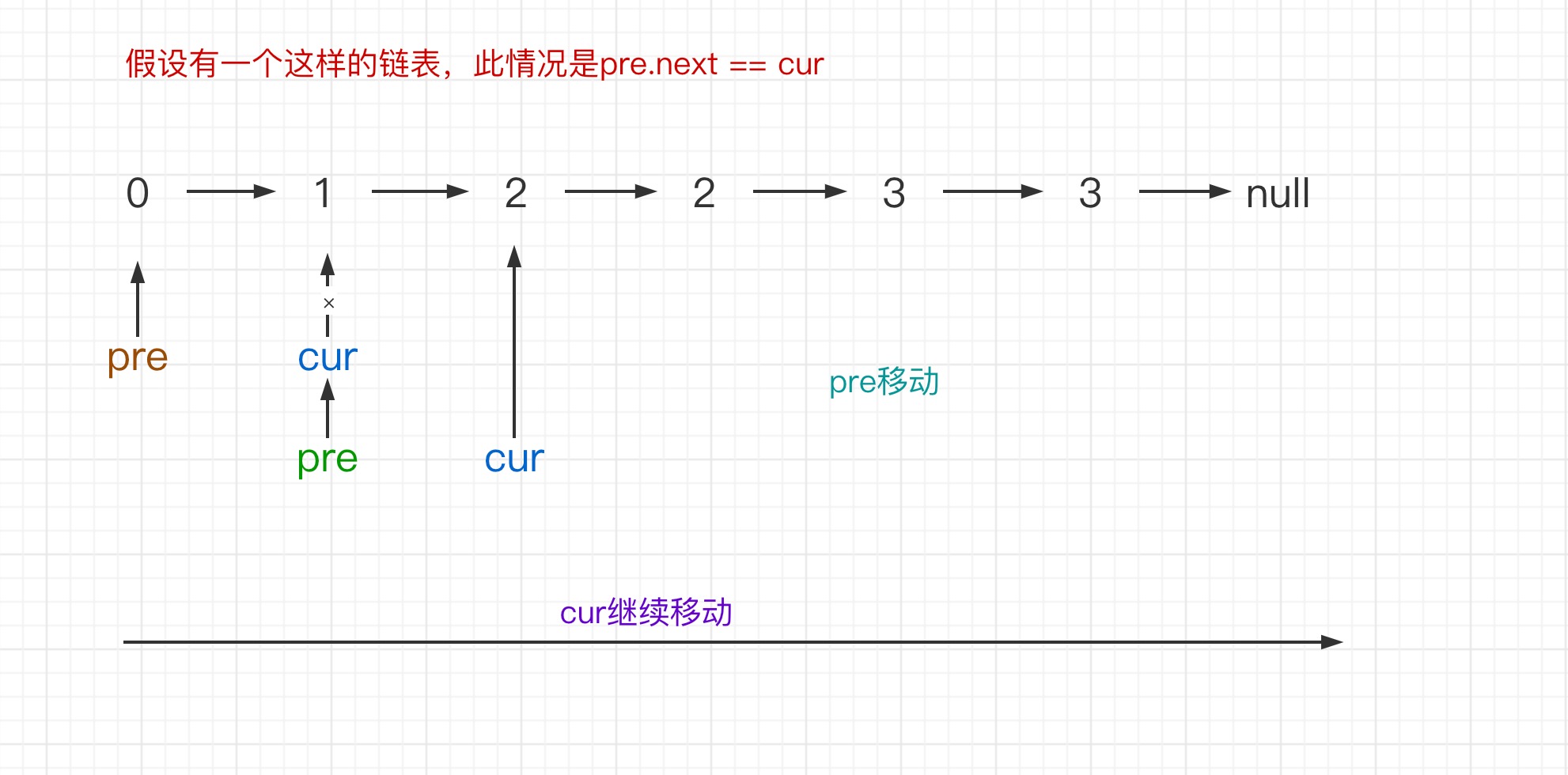
时间复杂度:O(n) 空间复杂度:O(1)
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var deleteDuplicates = function(head) {
let pre = new ListNode(0) //创建一个虚拟的节点指向head,有可能删除头节点,方便为后续操作。
pre.next = head
let res = pre //结果链表
let cur = head //当前节点,指向重复元素的最后一个节点
while(cur !== null){
while(cur.next !== null && cur.val === cur.next.val){
cur = cur.next //如果cur的next不为空,并且当前节点与后续节点值相同,继续向后移动
}
if(pre.next !== cur){/* 当前节点不是 pre 节点的下一节点,则将 pre 节点的下一节点指向当前节点的下一节点,相当于删除当前所有含跟当前节点值相等的节点 */
pre.next = cur.next
}else if(pre.next === cur){ //否则pre向右移动
pre = pre.next
}
cur = cur.next
}
return res.next
};88. 合并两个有序数组
给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中,使 nums1 成为一个有序数组。初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。你可以假设 nums1 的空间大小等于 m + n,这样它就有足够的空间保存来自 nums2 的元素。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
/**
* @param {number[]} nums1
* @param {number} m
* @param {number[]} nums2
* @param {number} n
* @return {void} Do not return anything, modify nums1 in-place instead.
*/
var merge = function(nums1, m, nums2, n) {
// 声明两个指针
let p1 = 0, p2 = 0;
// 临时数组
const sorted = [];
// 当前元素值
var cur;
while (p1 < m || p2 < n) {
// 如果nums1遍历结束
if (p1 === m) {
cur = nums2[p2++];
} else if (p2 === n) {
// 如果nums2遍历结束
cur = nums1[p1++];
} else if (nums1[p1] < nums2[p2]) {
cur = nums1[p1++];
} else {
cur = nums2[p2++];
}
sorted.push(cur);
}
for (let i = 0; i != m + n; ++i) {
nums1[i] = sorted[i];
}
};99. 恢复二叉搜索树
给你二叉搜索树的根节点 root ,该树中的两个节点被错误地交换。请在不改变其结构的情况下,恢复这棵树。
示例1:输入:root = [1,3,null,null,2],输出:[3,1,null,null,2]
解释:3 不能是 1 左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例 2:输入:root = [3,1,4,null,null,2],输出:[2,1,4,null,null,3]
解释:2 不能在 3 的右子树中,因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。
解题思想1:二叉搜索树利用中序遍历的结果是一个递增数列。找到两个错误节点的位置(两种情况,两节点相邻和不相邻),然后交换的两个节点的值。时间复杂度O(n) 空间复杂度(h) h是递归栈的深度。
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {void} Do not return anything, modify root in-place instead.
*/
var recoverTree = (root) => {
// 前一个节点元素,初始值为最小值(需要注意数据范围)
let pre = new TreeNode(-Infinity);
// 错误位置1 and 2
let err1, err2 = null;
const inOrder = (node) => {
if (node === null) {
return;
}
inOrder(node.left);
// 如果前一个元素大于当前元素并且错误位置1为空
if (pre.val >= node.val && err1 === null) {
// 记录错误位置1
err1 = pre;
}
// 如果前一个元素大于当前元素并且错误位置1不为空
if (pre.val >= node.val && err1 !== null) {
// 记录错误位置2
err2 = node;
}
// 更新pre
pre = node;
inOrder(node.right);
};
// 函数调用
inOrder(root);
// 交换两个错误位置节点值
let temp = err1.val;
err1.val = err2.val;
err2.val = temp;
};解题思想2:Morris 遍历算法
假设当前节点为root,初始值为root。
1.cur无左树,cur直接向右移动,cur = cur.right
2.cur有左树,找到左树最右节点设为mostRight
(1)mostRight的右指针指向null的话,mostRight的右指针指向当前节点,mostRight.right = cur, 然后cur向左移动,cur = cur.left
(2)mostRight的右指针指向cur(第一步操作的结果),mostRight.right = null,cur = cur.right,向右移动
3.cur = null流程截止
时间复杂度O(n) 空间复杂度(1)
var recoverTree = function(root) {
let err1 = null, err2 = null, pre = null, mostRight = null
// 如果root不为空
while (root !== null) {
// 如果节点含有左子树
if (root.left !== null) {
// 找到左树最右节点设为mostRight
mostRight = root.left
while (mostRight.right !== null && mostRight.right !== root) {
mostRight = mostRight.right
}
// mostRight的右指针指向null的话,mostRight的右指针指向当前节点,然后root向左移动
if (mostRight.right === null) {
mostRight.right = root
root = root.left
} else {
// 如果前一个元素大于当前元素
if (pre !== null && root.val < pre.val) {
err2 = root
// 错误位置1为空
if (err1 === null) {
err1 = pre
}
}
// 更新pre
pre = root
// mostRight的右指针指向root,向右移动
mostRight.right = null
root = root.right
}
}else {
// 如果前一个元素大于当前元素
if (pre !== null && root.val < pre.val) {
err2 = root
// 错误位置1不为空
if (err1 === null) {
err1 = pre
}
}
pre = root
// root无左树,root直接向右移动
root = root.right
}
}
// 交换两个错误位置节点的值
let temp = err1.val
err1.val = err2.val
err2.val = temp
};101 对称二叉树
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3子树对称条件:
他们两个的根结点具有相同的值;
每个树的右子树都与另一个树的左子树镜面对称;
解题思想1:根据子树对称条件进行解决。递归法 时间复杂度O(n) 空间复杂度o(n)
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isSymmetric = function(root) {
return isSimilar(root,root)
};
/**判断是否对称 */
const isSimilar = (tree1,tree2)=>{
if(tree1 == null && tree2 === null){
//如果两个子树都为空
return true
}
if(tree1 == null || tree2 === null){
return false //其中一个子树为空
}
return (tree1.val === tree2.val) && isSimilar(tree1.right,tree2.left) && isSimilar(tree1.left,tree2.right) //子树节点有值并且互为对称
}解题思想2:根据子树对称条件进行解决。迭代法 时间复杂度O(n) 空间复杂度O(n)
var isSymmetric = function(root) {
let queue = [root,root]
while(queue.length > 0){
let tree1 = queue.shift() //取队头元素
let tree2 = queue.shift()
if(tree1 == null && tree2 === null){
//如果两个子树都为空
continue
}
if(tree1 == null || tree2 === null){
return false //其中一个子树为空
}
if(tree1.val !== tree2.val){
return false
}
queue.push(tree1.left)
queue.push(tree2.right)
queue.push(tree1.right)
queue.push(tree2.left)
}
return true
};102 二叉树的层序遍历
给你一个二叉树,请你返回其按层序遍历得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例:二叉树:[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7返回其层序遍历结果:
[
[3],
[9,20],
[15,7]
]解题思想1:广度优先遍历二叉树,遍历过程中,记录每个节点的层级,并将其添加到不同的数组中,利用队列来实现。 时间复杂度 O(n) 空间复杂度为 O(n)
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
/**102. 二叉树的层序遍历 bfs */
var levelOrder = function(root) {
let res = [] //用于返回结果
if (root === null) {
return res
}
let queue = [] // 初始化数组队列
queue.push(root) // 将root加入queue中
while (queue.length > 0) { // queue中有元素,开启新的层级
size = queue.length // 当前层有多少元素
let list = [] // 存储每一层上的元素
while (size > 0) {
// 遍历当层所有元素
let cur = queue.shift() // cur用于存储从queue中取出的数
list.push(cur.val) // 将cur的值加进list中
if (cur.left !== null) {
queue.push(cur.left) // 如果此节点的左子树存在,就把他加进queue中,因为他是下一层的元素
}
if (cur.right !== null) {
queue.push(cur.right)
}
--size // 跳出循环
}
res.push(list) // 将每一层的数据放在结果数组中
}
return res
};解题思想2:深度优先遍历
var levelOrder = function(root) {
let res = [] //用于返回结果
if (root === null) {
return res
}
dfs(root, res, 0)
return res
};
/**
* @param {TreeNode} node 当前节点
* @param {number} level 当前层级
* @param {number[][]} result 结果集
*
*/
const dfs = (node, result, level) => {
if (node === null) {
return
}
if (level > result.length - 1) {
result.push([]) // 存储当前层级的结果集
}
result[level].push(node.val)
if (node.left !== null) {
dfs(node.left, result, level +1)
}
if (node.right !== null) {
dfs(node.right, result, level +1)
}
}103. 二叉树的锯齿形层序遍历
给定一个二叉树,返回其节点值的锯齿形层序遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
例如:给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7返回锯齿形层序遍历如下:
[
[3],
[20,9],
[15,7]
]解题思想1:深度优先遍历:递归,相同层序的节点放入同一个数组中,传入辅助的level参数,决定层序,根据层次的奇偶性判断遍历方向。时间复杂度O(n) 空间复杂度O(n)
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
var zigzagLevelOrder = function(root) {
let res = [] // 结果数组
if (root === null) {
return res
}
levelOrder(root, 0, res)
return res
};
/**
* @param {TreeNode} node 节点
* @param {number} level 层序
* @param {number[][]} res 结果数组
*/
function levelOrder(node, level, res) {
if( node === null) {
return []
}
if (level === res.length) {
// 如果level等于res的长度(当根节点为第0层)
let cur = [] // 存储当前层的节点
cur.push(node.val)
res.push(cur) // 放入结果集中
}else {
if (level % 2 === 0) {
res[level].push(node.val) // 根据level层序,将节点加入对应层。根据层序的奇偶性确定加入的位置
}else {
res[level].unshift(node.val)
}
}
// 递归
if (node.left !== null) {
levelOrder(node.left, level + 1, res)
}
if (node.right !== null) {
levelOrder(node.right, level + 1, res)
}
}解题思想2:广度优先遍历,时间复杂度O(n) 空间复杂度O(n)
var zigzagLevelOrder = function(root) {
let res = [] //用于返回结果
if (root === null) {
return res
}
let queue = [] // 初始化数组
queue.push(root)
let isOrderLeft = true
while (queue.length > 0) { // 外循环开启新的层级
size = queue.length // 当前层有多少元素
let list = [] // 存储每一层上的元素
while (size > 0) {
// 遍历当层所有元素
let cur = queue.shift() // cur用于存储从queue中取出的数
// 将cur的值加进list中
if (isOrderLeft) {
list.push(cur.val); // 从左往右存数据
} else {
list.unshift(cur.val); // 从右往左存数据
}
if (cur.left !== null) {
queue.push(cur.left) // 如果此节点的左子树存在,就把他加进queue中,因为他是下一层的元素
}
if (cur.right !== null) {
queue.push(cur.right)
}
--size // 跳出循环
}
res.push(list) // 将每一层的数据放在结果数组中
isOrderLeft = !isOrderLeft // 修改遍历的方向
}
return res
};104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7解题思想:bfs
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var maxDepth = function(root) {
if (root === null) {
return 0
}
let res = 0
let queue = []
queue.push(root)
while (queue.length > 0) {
let len = queue.length
while (len > 0) {
let cur = queue.pop()
if (cur.left !== null) {
queue.push(cur.left)
}
if (cur.right !== null) {
queue.push(cur.right)
}
len--
}
res++
}
return res
};105 从前序与中序遍历序列构造二叉树
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树
3
/ \
9 20
/ \
15 7解题思想1:前序遍历的第一个节点一定是二叉树的根节点。在中序遍历中,根节点把中序遍历序列分成了两个部分,左边构成了二叉树的的根节点的左子树,右边部分构成了二叉树的根节点的右子树。时间复杂度 O(n) 空间复杂度 O(n)。

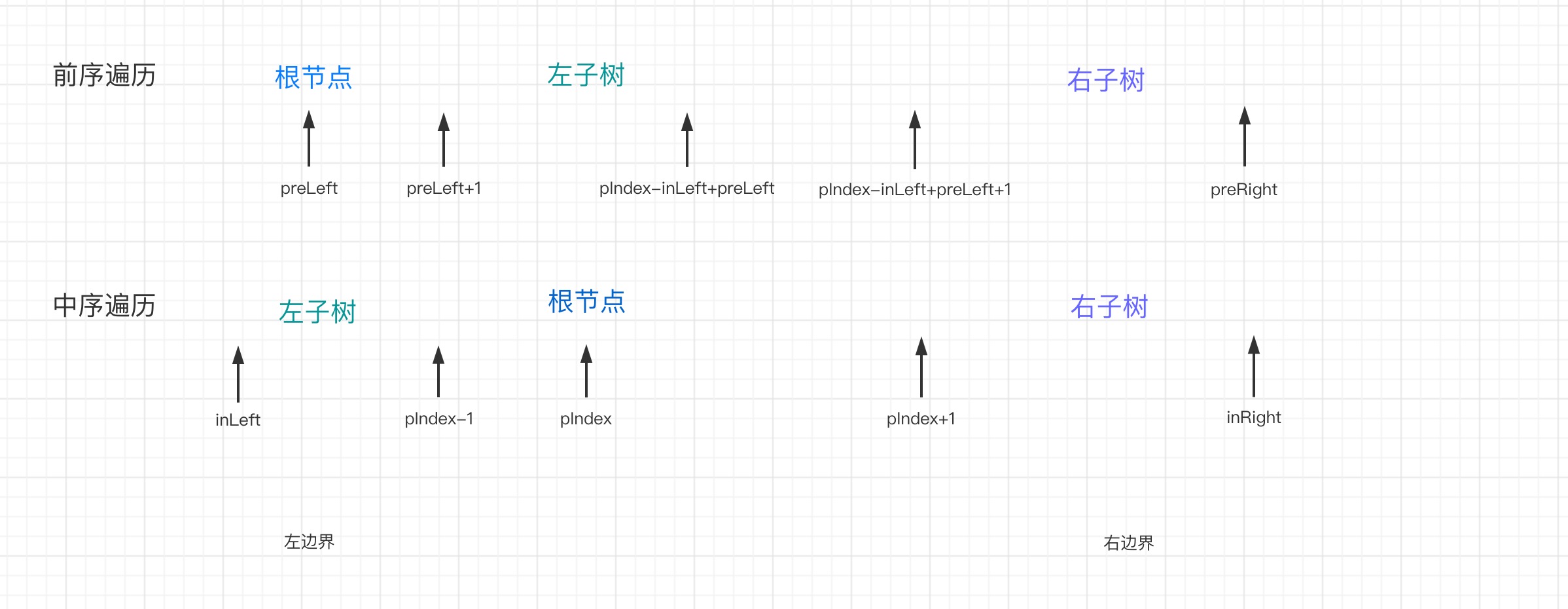
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} preorder
* @param {number[]} inorder
* @return {TreeNode}
*/
/**105. 从前序与中序遍历序列构造二叉树 */
var buildTree = function(preorder, inorder) {
let preLen = preorder.length // 前序遍历数组长度
let inLen = inorder.length //中序遍历数组长度
if (preLen === 0 || inLen === 0) {
return null
}
let map = new Map() //存储中序遍历的值和下标,方便后续操作
for(let i = 0; i < inLen; i++) {
// 将中序遍历的数组和下标用map存起来
map.set(inorder[i],i)
}
console.log('map',map)
return createTree(preorder, 0, preLen - 1, map, 0, inLen - 1)
};
/**
* @param {number[]} preorder 前序遍历
* @param {number} preLeft 前序遍历左边界
* @param {number} preRight 前序遍历右边界
* @param {Map} map 中序遍历的值和下标
* @param {number} inLeft 中序遍历左边界
* @param {number} inRigth 中序遍历右边界
* @return {TreeNode}
*/
function createTree(preorder, preLeft, preRight, map, inLeft, inRight) {
if (preLeft > preRight || inLeft > inRight) {
return null // 终止条件,区间没有值
}
//前序遍历中找到根节点
let rootVal = preorder[preLeft]
let root = new TreeNode(rootVal)
// 前序遍历的根节点在中序遍历中的位置
let pIndex = map.get(rootVal)
root.left = createTree(preorder, preLeft + 1, pIndex - inLeft + preLeft, map, inLeft, pIndex - 1)
root.right = createTree(preorder, pIndex - inLeft + preLeft + 1, preRight, map, pIndex + 1, inRight)
return root
}解题思想2:利用自身的函数递归。
var buildTree = function(preorder, inorder) {
let preLen = preorder.length // 前序遍历数组长度
let inLen = inorder.length //中序遍历数组长度
if (preLen === 0 || inLen === 0) {
return null
}
let map = new Map()
for(let i = 0; i < inLen; i++) {
// 将中序遍历的数组和下标用map存起来
map.set(inorder[i],i)
}
// 前序遍历中找到根节点
let rootVal = preorder[0]
let root = new TreeNode(rootVal)
// 前序遍历的根节点在中序遍历中的位置
let pIndex = map.get(rootVal)
root.left = buildTree(preorder.slice(1,pIndex+1),inorder.slice(0,pIndex))
root.right = buildTree(preorder.slice(pIndex+1),inorder.splice(pIndex+1))
return root
};106 从中序与后序遍历序列构造二叉树
根据一棵树的中序遍历与后序遍历构造二叉树。
注意:你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7解题思想:后序遍历的最后一个节点一定是二叉树的根节点。在中序遍历中,根节点把中序遍历序列分成了两个部分,左边构成了二叉树的的根节点的左子树,右边部分构成了二叉树的根节点的右子树。时间复杂度 O(n) 空间复杂度 O(n)。


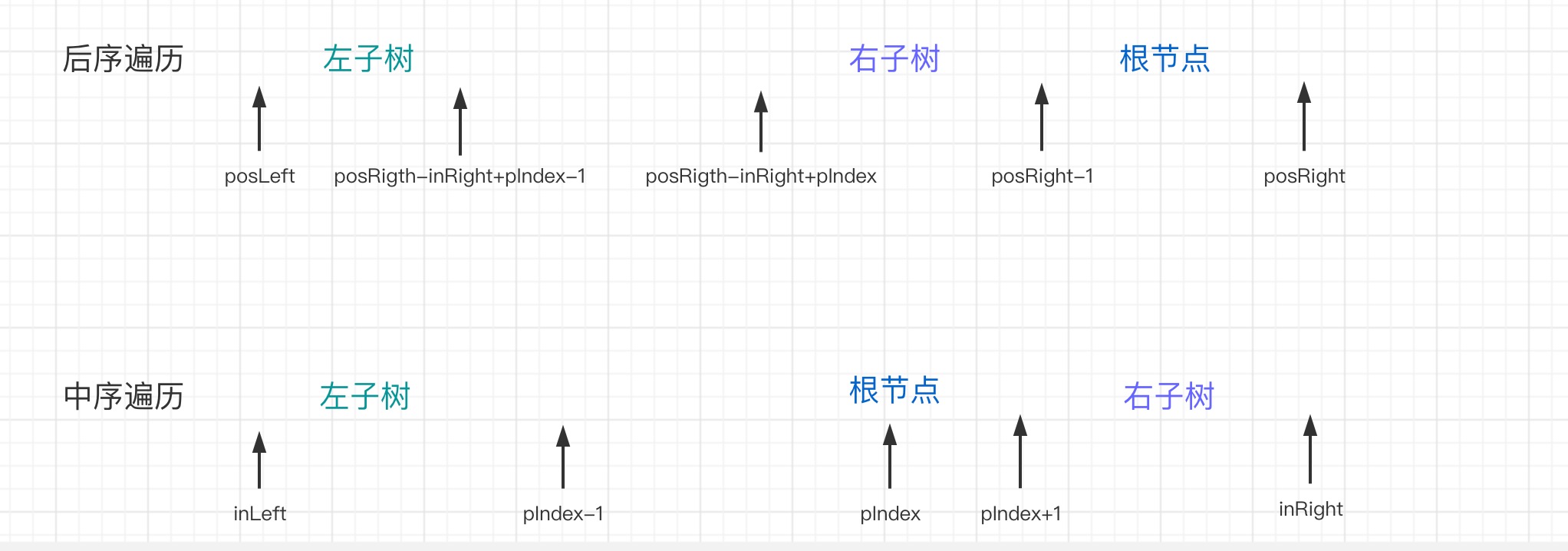
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} inorder
* @param {number[]} postorder
* @return {TreeNode}
*/
/**106. 从中序与后序遍历序列构造二叉树 */
var buildTree = function(inorder, postorder) {
let inLen = inorder.length // 中序遍历数组长度
let posLen = postorder.length // 后序遍历数组长度
if (inLen === 0 || posLen === 0) {
return null
}
let map = new Map() // 保存中序遍历数组的值和下标
for(let i = 0; i < inLen; i++) {
map.set(inorder[i],i)
}
return createTree(postorder, 0, posLen - 1, map, 0, inLen - 1)
};
/**
* @param {number[]} postorder 前序遍历
* @param {number} posLeft 前序遍历左边界
* @param {number} posRight 前序遍历右边界
* @param {Map} map 后序遍历的值和下标
* @param {number} inLeft 后序遍历左边界
* @param {number} inRigth 后序遍历右边界
* @return {TreeNode}
*/
function createTree(postorder, posLeft, posRight, map, inLeft, inRight) {
if (posLeft > posRight || inLeft > inRight) {
return null // 终止条件,区间没有值
}
//前序遍历中找到根节点
let rootVal = postorder[posRight]
let root = new TreeNode(rootVal)
// 前序遍历的根节点在后序遍历中的位置
let pIndex = map.get(rootVal)
root.left = createTree(postorder, posLeft, posRight - inRight + pIndex - 1, map, inLeft, pIndex - 1)
root.right = createTree(postorder, posRight - inRight + pIndex, posRight - 1, map, pIndex + 1, inRight)
return root
}108 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按升序排列,请你将其转换为一棵高度平衡二叉搜索树。
高度平衡二叉树是一棵满足每个节点的左右两个子树的高度差的绝对值不超过1的二叉树。
示例 1:输入:nums = [-10,-3,0,5,9],输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:输入:nums = [1,3],输出:[3,1]
解释:[1,3] 和 [3,1] 都是高度平衡二叉搜索树。
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
解题思想:分治法:把一个大问题分解成一个个小问题,每个小问题都有一个解,把所有解合并起来就是问题的解。用到了递归。先找到数组元素的中间节点作为根节点,对于数组中间节点左边的元素去求一个高度平衡的二叉树,对于数组中间节点右边的元素去求一个高度平衡的二叉树。时间复杂度:O(n) 空间复杂度:O(logn)
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} nums
* @return {TreeNode}
*/
/**108. 将有序数组转换为二叉搜索树 */
var sortedArrayToBST = function(nums) {
let root = findBST(nums, 0, nums.length - 1)
return root
};
/**
* @param {number[]} nums 数组
* @param {number} left 左边界
* @param {number} right 右边界
* @return {TreeNode}
*/
/**构造二叉搜索树 */
function findBST(nums, left, right){
if (left > right) {
// 左大于右,两个指针错开,说明这个区间没有
return null
}
let mid = parseInt((left + right) / 2) // 求中间节点的索引
let root = new TreeNode(nums[mid]) // 作为这一段树的根节点
root.left = findBST(nums, left, mid - 1)
root.right = findBST(nums, mid+1, right)
return root
}111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。说明:叶子节点是指没有子节点的节点。
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth = function(root) {
if (root === null) {
return 0;
}
if (root.left === null && root.right === null) {
return 1;
}
let queue = [];
queue.push(root);
let res = 1;
while(queue.length > 0) {
let size = queue.length;
for (let i = 0; i < size; i++) {
let cur = queue.shift();
if (cur.left === null && cur.right === null) {
return res;
}
if (cur.left !== null) {
queue.push(cur.left);
}
if (cur.right !== null) {
queue.push(cur.right);
}
}
res++;
}
return res;
};112 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ,判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。叶子节点是指没有子节点的节点。
示例 1:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:false
示例 3:
输入:root = [1,2], targetSum = 0
输出:false
解题思想1:广度优先搜索,记录从根节点到当前节点的路径和,防止重复计算。可以使用两个队列,分别存储将要遍历的节点,以及根节点到这些节点的路径和。时间复杂度O(n) 空间复杂度O(n)
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {boolean}
*/
/**112. 路径总和 */
var hasPathSum = function(root, targetSum) {
if (root === null) {
return false // 判断根节点是否存在
}
let queueNode = [] // 队列,存储节点
queueNode.push(root)
let queueVal = [] // 队列,存储节点的值
queueVal.push(root.val)
while(queueNode.length > 0) {
let cur = queueNode.shift() //取出节点
let val = queueVal.shift() // 取出节点的值
if (cur.left === null && cur.right === null) { //如果节点不存在子节点(是叶子节点)
if (val === targetSum) { // 判断路径和和目标值是否相等,不相等迭代继续执行
return true
}
continue
}
if (cur.left !== null) {
// 如果当前节点有左子节点,将左子节点加入队列
queueNode.push(cur.left)
queueVal.push(cur.left.val + val)
}
if (cur.right !== null) {
// 如果当前节点有右子节点,将左子节点加入队列
queueNode.push(cur.right)
queueVal.push(cur.right.val + val)
}
}
return false
};解题思想2:深度优先搜索 假定从根节点到当前节点的值之和为val,我们可以将这个问题转化为一个:是否存在从当前节点的子节点到叶子的路径,满足其路径和为sum-val 。若当前节点是叶子节点,判断sum是否等于val,若当前节点不是叶子节点,递归判断他的子节点是否能满足条件。 时间复杂度O(n) 空间复杂度O(n)。
/**112. 路径总和 */
var hasPathSum = function(root, targetSum) {
if (root === null) {
return false // 判断根节点是否存在
}
if (root.left === null && root.right === null) {
// 如果是叶子节点,判断当前值和目标值是否相等
return targetSum === root.val
}
// 递归分别传入当前节点的左/右子节点和目标值
return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.root, targetSum - root.val)
}114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
展开后的单链表应该与二叉树先序遍历顺序相同。
示例 1:
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:输入:root = [],输出:[]
示例 3:输入:root = [0],输出:[0]
解题思想:采用后序遍历的方式,也就是 左节点-右节点-打印根节点 这个顺序遍历二叉树。当遍历到根节点后,对根节点的左右子树做一些调整,将右节点挂到左节点的最右边,再将整个左子树挂到根节点的右边,这样就可以将整棵树变成链表结构了。 时间复杂度O(n) 空间复杂度O(h) h是树高度。
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {void}
*/
var flatten = function(root) {
if (root === null) {
return null
}
list(root)
};
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
function list(root) {
if (root === null) {
return null
}
let left = list(root.left) // 左子树
let right = list(root.right) // 右子树
if (left === null) {
root.right = right // 如果左子树为空,节点的right指针指向右子树
} else {
root.right = left // 右指针指向左子树
let cur = left
while(cur.right !== null) {
cur = cur.right // 找到左子树最右节点
}
cur.right = right //令左子树中的最右节点的右指针指向根节点的右子树
root.left = null // 令二叉树的左子树为空
}
return root
}116. 填充每个节点的下一个右侧节点指针
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例1:输入:root = [1,2,3,4,5,6,7],输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,’#’ 标志着每一层的结束。
解题思想:第一种情况两个子节点属于同一个父节点,直接通过父节点建立两个子节点的 next 指针。node.left.next = node.right。第二种情况是连接不同父节点之间子节点的情况。连接的是第一个父节点的右孩子和第二父节点的左孩子。可以直接通过第一个父节点的 next 指针找到第二个父节点,然后在它们的孩子之间建立连接。node.right.next = node.next.left。时间复杂度O(n) 空间复杂度O(h) h是树高度
/**
* // Definition for a Node.
* function Node(val, left, right, next) {
* this.val = val === undefined ? null : val;
* this.left = left === undefined ? null : left;
* this.right = right === undefined ? null : right;
* this.next = next === undefined ? null : next;
* };
*/
/**
* @param {Node} root
* @return {Node}
*/
var connect = function(root) {
if (root === null) {
return null
}
// 如果是叶子节点
if (root.left === null && root.right === null) {
return root
}
// next指针指向其下一个右侧节点
root.left.next = root.right
// 如果右侧节点存在,处理不同父节点之间子节点的情况
if (root.next !== null) {
// 连接的是第一个父节点的右孩子和第二父节点的左孩子。
root.right.next = root.next.left
}
// 递归
connect(root.left)
connect(root.right)
return root
};117. 填充每个节点的下一个右侧节点指针 II
给定一个二叉树
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
输入:root = [1,2,3,4,5,null,7]
输出:[1,#,2,3,#,4,5,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),’#’ 表示每层的末尾。
解题思想:此题二叉树不再是完美二叉树,是一棵普通的二叉树。使用广度优先搜索,初始化一个队列,将根结点放入队列中。当队列不为空的时候,记录当前队列大小为len,从队列中取出len个元素并通过这len个元素拓展新节点。如此循环,直到队列为空。在遍历每一层的时候修改这一层节点的next指针。时间复杂度O(n) 空间复杂度O(n)
/**
* // Definition for a Node.
* function Node(val, left, right, next) {
* this.val = val === undefined ? null : val;
* this.left = left === undefined ? null : left;
* this.right = right === undefined ? null : right;
* this.next = next === undefined ? null : next;
* };
*/
/**
* @param {Node} root
* @return {Node}
*/
var connect = function(root) {
if (root === null) {
return null;
}
// 定义一个队列
let queue = []
// 将根节点放入队列
queue.push(root)
while (queue.length > 0) {
// 队列长度
let len = queue.length;
let last = null;
// 遍历当前层所有元素
for (let i = 0; i < len; i++) {
//取出元素
let cur = queue.shift();
if (cur.left !== null) {
queue.push(cur.left);
}
if (cur.right !== null) {
queue.push(cur.right);
}
// 修改这一层节点的next指针,
if (i !== 0) {
last.next = cur;
}
last = cur;
}
}
return root;
};138 复制带随机指针的链表
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random –> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random –> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示 Node.val 的整数。
random_index:随机指针指向的节点索引(范围从 0 到 n-1);如果不指向任何节点,则为 null 。
你的代码 只 接受原链表的头节点 head 作为传入参数。
解题思想:利用Map存储新链表与旧链表之间random一一对应的关系,两个循环进行实现,一个循环用于拷贝链表普通属性next、val,并且记录random指针所对应的关系,一个循环按照记录的关系对random进行赋值。时间复杂度:O(n) 空间复杂度:O(n)
/**
* // Definition for a Node.
* function Node(val, next, random) {
* this.val = val;
* this.next = next;
* this.random = random;
* };
*/
/**
* @param {Node} head
* @return {Node}
*/
var copyRandomList = function(head) {
if(head === null){
return head
}
let cur = head //当前指针
let node = new Node() //新的链表
let temp = node
let map = new Map() //用于存储新链表与旧链表之间random一一对应的关系
//此循环用于拷贝链表普通属性next、val,并且记录random指针所对应的关系
while(cur !== null){
temp.val = cur.val
temp.next = cur.next ? new Node() : null
map.set(cur,temp) //存储一一对应的关系
temp = temp.next
cur = cur.next
}
temp = node //指针重新回到头部
cur = head
//此循环按照记录的关系对random进行赋值
while(cur !== null){
temp.random = cur.random ? map.get(cur.random) : null //判断旧链表中当前节点是否存在random
cur = cur.next
temp = temp.next
}
return node
};141. 环形链表
给定一个链表,判断链表中是否有环。如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。如果链表中存在环,则返回 true 。 否则,返回 false 。
进阶:你能用 O(1)(即,常量)内存解决此问题吗?
解题思想1:使用 map 保存每个节点,判断 map 中节点是否已经含有,若有则有环。
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {boolean}
*/
/**使用map */
var hasCycle = function(head) {
if (head === null || head.next === null) {
return false;
}
let cur = head;
let map = new Map();
while (cur !== null) {
if(map.has(cur)) {
return true;
}
map.set(cur, cur.val);
cur = cur.next;
}
return false;
};解题思想2:使用快慢指针,快指针移动两步,慢指针移动一步,在移动过程中若两者相等,则有环。
var hasCycle = function(head) {
if (head === null || head.next === null) {
return false;
}
let slow = head, fast = head;
while (fast !== null && fast.next !== null) {
fast = fast.next.next;
slow = slow.next;
if (fast === slow) {
return true;
}
}
return false;
};146. LRU 缓存机制
运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制 。
实现 LRUCache 类:
LRUCache(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字-值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
示例:
输入
[“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4解题思想:改变数据访问时间,需要能随机访问,需要把该数据插入到头部或者尾部。
/**
* @param {number} capacity
*/
var LRUCache = function(capacity) {
this.capacity = capacity
// 保存键、值
this.map = new Map()
};
/**
* @param {number} key
* @return {number}
*/
LRUCache.prototype.get = function(key) {
// 获取键的值
let value = this.map.get(key)
// 如果不含有这个键,就返回-1
if (value === undefined) {
return -1
}
// 寻找是否有记录
this.map.delete(key); // 因为被用过一次,原有位置删除
this.map.set(key, value); // 放入最下面表示最新使用
return value
};
/**
* @param {number} key
* @param {number} value
* @return {void}
*/
LRUCache.prototype.put = function(key, value) {
// 如果存在元素
if (this.map.has(key)) {
// 先删除
this.map.delete(key)
}
// 放到最下面表示最新使用
this.map.set(key,value)
// map中元素个数大于容量,就一个个删除
if (this.map.size > this.capacity) {
// 迭代器
let keyIterator = this.map.keys();
// 迭代器调用next顺序返回
this.map.delete(keyIterator.next().value);
}
};162. 寻找峰值
峰值元素是指其值大于左右相邻值的元素。给你一个输入数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。你可以假设 nums[-1] = nums[n] = -∞ 。
示例 1:输入:nums = [1,2,3,1],输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:输入:nums = [1,2,1,3,5,6,4],输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;或者返回索引 5, 其峰值元素为 6。
解题思想1:直接遍历 时间复杂度O(n) 时间复杂度O(1)
/**
* @param {number[]} nums
* @return {number}
*/
var findPeakElement = function(nums) {
nums[nums.length] = Number.NEGATIVE_INFINITY
for (let i = 0; i < nums.length; i++) {
if (i - 1 > 0) {
if (nums[i] > nums[i+1] && nums[i] > nums[i-1]) {
return i
}
} else {
if(nums[i] > nums[i+1] && nums[i] > Number.NEGATIVE_INFINITY) {
return i
}
}
}
};解题思想2:二分迭代 时间复杂度O(log(2)n) 时间复杂度O(1)
var findPeakElement = function(nums) {
let left = 0, right = nums.length - 1, mid
while (left < right) {
mid = Math.floor((left + right) / 2)
if (nums[mid] > nums[mid + 1]) {
right = mid
} else {
left = mid + 1
}
}
return left
};165. 比较版本号
给你两个版本号 version1 和 version2 ,请你比较它们。
版本号由一个或多个修订号组成,各修订号由一个 ‘.’ 连接。每个修订号由 多位数字 组成,可能包含 前导零 。每个版本号至少包含一个字符。修订号从左到右编号,下标从 0 开始,最左边的修订号下标为 0 ,下一个修订号下标为 1 ,以此类推。例如,2.5.33 和 0.1 都是有效的版本号。
比较版本号时,请按从左到右的顺序依次比较它们的修订号。比较修订号时,只需比较 忽略任何前导零后的整数值 。也就是说,修订号 1 和修订号 001 相等 。如果版本号没有指定某个下标处的修订号,则该修订号视为 0 。例如,版本 1.0 小于版本 1.1 ,因为它们下标为 0 的修订号相同,而下标为 1 的修订号分别为 0 和 1 ,0 < 1 。
返回规则如下:
如果 version1 > version2 返回 1,
如果 version1 < version2 返回 -1,
除此之外返回 0。
示例 1:输入:version1 = “1.01”, version2 = “1.001”,输出:0
解释:忽略前导零,”01” 和 “001” 都表示相同的整数 “1”
示例 2:输入:version1 = “1.0”, version2 = “1.0.0”,输出:0
解释:version1 没有指定下标为 2 的修订号,即视为 “0”
示例 3:输入:version1 = “0.1”, version2 = “1.1”,输出:-1
解释:version1 中下标为 0 的修订号是 “0”,version2 中下标为 0 的修订号是 “1” 。0 < 1,所以 version1 < version2
/**
* @param {string} version1
* @param {string} version2
* @return {number}
*/
var compareVersion = function(version1, version2) {
let v1 = version1.split('.');
let v2 = version2.split('.');
let l1 = v1.length;
let l2 = v2.length;
let n = Math.max(l1, l2);
let n1 = 0, n2 = 0;
for (let i = 0; i < n; i++) {
if (i < l1) {
n1 = parseInt(v1[i])
} else {
n1 = 0;
}
if (i < l2) {
n2 = parseInt(v2[i]);
} else {
n2 = 0;
}
if (n1 > n2) {
return 1;
} else if (n1 < n2) {
return -1;
}
}
return 0;
};189. 旋转数组
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
示例 1:输入: nums = [1,2,3,4,5,6,7], k = 3,输出: [5,6,7,1,2,3,4]
解释:向右旋转 1 步: [7,1,2,3,4,5,6]向右旋转 2 步: [6,7,1,2,3,4,5]向右旋转 3 步: [5,6,7,1,2,3,4]
示例 2:输入:nums = [-1,-100,3,99], k = 2,输出:[3,99,-1,-100]
解释: 向右旋转 1 步: [99,-1,-100,3]向右旋转 2 步: [3,99,-1,-100]
解题思想1:暴力求解(超出时间限制)
var rotate = function(nums, k) {
let len = nums.length;
// 可能会存在k大于数组长度
k = k % len;
for (let i = 0; i < k; i++) {
let n = nums[len - 1];
for (let j = len - 1; j > 0; j–) {
nums[j] = nums[j-1];
}
nums[0] = n;
}
};
解题思想2:翻转
var rotate = function(nums, k) {
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.length - 1);
}
function reverse(nums, start, end) {
while (start < end) {
let n = nums[start];
nums[start] = nums[end];
nums[end] = n;
end--;
start++;
}
}198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:输入:[1,2,3,1],输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:输入:[2,7,9,3,1],输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。
解题思想:动态规划,因为不可以在相邻的房屋闯入,所以在当前位置 n 房屋可盗窃的最大值,要么就是 n-1 房屋可盗窃的最大值,要么就是 n-2 房屋可盗窃的最大值加上当前房屋的值,dp[i] = Math.max(nums[i] + dp[i - 2], dp[i - 1]),二者之间取最大值。
/**
* @param {number[]} nums
* @return {number}
*/
var rob = function(nums) {
if (nums.length === 0) {
return 0;
} else if (nums.length === 1) {
return nums[0];
} else if (nums.length === 2) {
return Math.max(nums[0], nums[1]);
}
let dp = [nums[0],Math.max(nums[0], nums[1])];
for (let i = 2; i < nums.length; i++) {
dp[i] = Math.max(nums[i] + dp[i - 2], dp[i - 1]);
}
return Math.max(dp[nums.length - 1], dp[nums.length - 2]);
};199. 二叉树的右视图
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例:输入: [1,2,3,null,5,null,4],输出: [1, 3, 4]
解释:
1 <---
/ \
2 3 <---
\ \
5 4 <---解题思想1:广度优先搜索,进行层次遍历,利用map记录每层最后一个元素。时间复杂度O(n) 空间复杂度O(n)。
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var rightSideView = function(root) {
// 结果集
let res = []
if (root === null) {
return res
}
// 定义一个队列,放入节点
let queue = []
// 将根节点放入队列
queue.push(root)
// 定义一个队列放入depth
let queueDepth = []
queueDepth.push(0)
// 存放每层最右边的节点
let map = new Map()
while(queue.length > 0) {
// 取出元素
let cur = queue.shift()
let depth = queueDepth.shift()
if (!map.has(depth)) {
// 如果不存在对应深度的节点
map.set(depth, cur.val)
}
if (cur.right !== null) {
queue.push(cur.right)
queueDepth.push(depth + 1)
}
if (cur.left !== null) {
queue.push(cur.left)
queueDepth.push(depth + 1)
}
}
// 遍历map,将值放入res结果数组中
for(let value of map.values()) {
res.push(value)
}
return res
};解题思想2:深度优先搜索,按照根节点->右子树->左子树进行遍历,这样每次每层都是最先访问最右边的节点。时间复杂度O(n) 空间复杂度O(n)
var rightSideView = function(root) {
// 结果集
let res = []
if (root === null) {
return res
}
dfs(root, 0, res)
return res
}
/**
* @param {TreeNode} node // 节点
* @param {number} level // 层序
* @param {number[]} res // 结果
*/
function dfs(node, level, res) {
if (node === null) {
return res
}
//先访问当前节点
//如果当前节点所在层序没有出现在res中,说明在该层序下当前节点是第一个被访问的节点,则将当前节点加入res中
if (level === res.length) {
res.push(node.val)
}
//递归访问右子树和左子树
dfs(node.right, level + 1, res)
dfs(node.left, level + 1, res)
}206 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例1:输入:head = [1,2,3,4,5],输出:[5,4,3,2,1]
示例2:输入:head = [1,2],输出:[2,1]
示例3:输入:head = [],输出:[]
解题思想:当前项的next指向前一项。时间复杂度O(n),空间复杂度O(1)
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
/**反转链表:当前项的next指向前一项 */
var reverseList = function(head) {
//记录指针变量
let pre = null
let cur = head
while(cur){
let next = cur.next //先保存当前节点的next,防止断链
cur.next = pre
pre = cur
cur = next
}
return pre
};236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例1:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
/**时间复杂度O(n) 空间复杂度O(n) */
var lowestCommonAncestor = function(root, p, q) {
if (root === null) {
return null
}
let res = new TreeNode()
function dfs(root, p, q) {
if (node === null) {
return false
}
// 递归
let leftTree = dfs(root.left, p, q)
let rightTree = dfs(root.right, p, q)
// 左子树和右子树均包含p或q或者当前节点是p或q且它的左子树或右子树有一个包含了另一个节点的,判断当前节点是否可能成为最近的公共祖先
if ((leftTree && rightTree) || ((root.val === p.val || root.val === q.val) && (leftTree || rightTree))) {
// 记录公共祖先
res = root
}
// 判断当前节点子树是否分别包含p或q,如果是返回true,否则返回false
return (root.val === p.val || root.val === q.val) || (leftTree || rightTree)
}
// 函数调用
dfs(root, p, q)
return res
};300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:输入:nums = [10,9,2,5,3,7,101,18],输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:输入:nums = [0,1,0,3,2,3],输出:4
示例 3:输入:nums = [7,7,7,7,7,7,7],输出:1
/**
* @param {number[]} nums
* @return {number}
*/
var lengthOfLIS = function(nums) {
let len = nums.length
// 结果
let res = 0
let temp = []
for (let i = 0; i < len; i++) {
// 初始情况下递增子序列长度最小为1
let max = 1
for (let j = 0; j < i; j++) {
// 找到一个nums[i]比前序转移方程temp[j]最大值还要大,说明递增子序列还可以+1
if (nums[i] > nums[j]) {
max = Math.max(max, temp[j] + 1)
}
}
// 每一趟下标小于等于i的子序列遍历都能找到以i为结尾下标的最大递增子序列长度
temp[i] = max
}
console.log(temp)
// 遍历找到最大的temp[i]即结果
for (let i = 0; i < len; i++) {
res = Math.max(res, temp[i])
}
return res
};
var lengthOfLIS = function(nums) {
let len = nums.length,
dp = new Array(len).fill(1); // 用于保存长度
for (let i = len - 1; i >= 0; i--) {
let cur = nums[i]
for(let j = i + 1; j < len; j++) {
let next = nums[j]
// 如果是递增 取更大的长度值
if (cur < next) {
dp[i] = Math.max(dp[j]+1, dp[i])
}
}
}
return Math.max(...dp)
}322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬币的数量是无限的。
示例 1:输入:coins = [1, 2, 5], amount = 11,输出:3
解释:11 = 5 + 5 + 1
示例 2:输入:coins = [2], amount = 3,输出:-1
示例 3:输入:coins = [1], amount = 0,输出:0
解题思想:动态规划,金额为n时,硬币数等于(n-coin)+1中所需硬币最少的组合。
/**
* @param {number[]} coins
* @param {number} amount
* @return {number}
*/
/**322. 零钱兑换 */
var coinChange = function(coins, amount) {
// 因为存在0块钱,所以数组长度是amount + 1
let dp = new Array(amount + 1).fill( Infinity );
// dp[0] = 0 金额为零时不需要硬币
dp[0] = 0;
for (let i = 1; i <= amount; i++) {
for (let coin of coins) {
if (i - coin >= 0) {
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
}
return dp[amount] === Infinity ? -1 : dp[amount];
};343. 整数拆分
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:输入: 2,输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:输入: 10,输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
/**
* @param {number} n
* @return {number}
*/
var integerBreak = function(n) {
if (n < 2) {
return 0;
}
if (n === 2) {
return 1;
}
if (n === 3) {
return 2;
}
let a = n % 3;
let b = parseInt(n / 3);
if(a === 0){
return Math.pow(3, b);
}else if(a === 1){
return 2 * 2 * Math.pow(3, b - 1);;
}else{
return 2 * Math.pow(3, b);
}
};718. 最长重复子数组
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例:
输入:A: [1,2,3,2,1],B: [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3, 2, 1] 。
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number}
*/
var findLength = function(nums1, nums2) {
let dp = new Array
for (let i = 0; i < nums1.length; i++) {
dp[i] = new Array()
// dp为二维数组
for (let j = 0; j < nums2.length; j++) {
dp[i][j] = new Array()
}
}
let res = 0
for (let i = 0; i < nums1.length; i++) {
for (let j = 0; j < nums2.length; j++) {
// 如果两者相等
if (nums1[i] === nums2[j]) {
if (i - 1 < 0 || j - 1 < 0) {
dp[i][j] = 1
} else {
dp[i][j] = dp[i - 1][j - 1] + 1
}
} else {
dp[i][j] = 0
}
res = Math.max(res, dp[i][j])
}
}
return res
};- 本文作者: étoile
- 版权声明: 本作品采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议 进行许可。转载请注明出处!

